This versatile Brushless (BLDC) motor controller IC is featured to control any desired high voltage, high current, hall effect sensor equipped 3-phase BLDC motor with extreme accuracy and safety. I will explain the details in depth.

Using the IC MC33035
The "hero" of the circuit is the single chip controller MC33035 which is a high performance second generation IC module, featuring all the required active functions that may be required to run most high current, high voltage, 3-phase or 4-phase BLDC motors with an open loop or a closed loop configuration.

The IC is equipped with a rotor position decoder for enabling an accurate commutation sequencing, temperature compensated reference for facilitating correct sensor voltage, a programmable frequency sawtooth oscillator, three in-built open collector high-side driver stages, and three high current totem-pole type low-side drivers, specifically designed to operate an 3-phase H-bridge high power mosfet motor controller stage.
The chip is also internally bolstered with high end protection features, and foolproof controls stages such as under-voltage lockout, cycle-by-cycle current limiting through an option of adjustable delay latched shutdown, internal IC high temperature shut down, and an exclusively devised fault output pinout which may be interfaced with an MCU for a preferred advanced processing and feed backs.
Typical functions that can be executed with this IC are, open loop speed control, forward reverse direction control, "run enable", an emergency dynamic brake feature.
The IC is designed to work with motor sensors having phases of 60 to 300 degrees or 120 to 240 degrees, as a bonus the IC can eb also used for controlling the traditional brushed motors.
How the IC Works
The MC33035 is amongst several high efficiency monolithic DC brushless motor controllers created by Motorola.
It's made up of just about the capabilities necessary to instigate a full−featured, open loop, three or four phase motor control system.
Furthermore, the controller can be accomplished to control DC brush motors. Designed with Bipolar Analog technology, it features a superior level of efficiency and durability in ruthless industrialized surroundings.
The MC33035 carries a rotor position decoder for accurate commutation sequencing, a environment reimbursed reference competent at delivering a sensor power, a frequency programmable sawtooth oscillator, a fully accessible error amplifier, a pulse width modulator comparator, 3 open collector top drive outputs, and 3 high current totem pole lower driver outputs just right for operating power MOSFETs.
Built into the MC33035 are shielding capabilities which includes undervoltage lockout, cycle−by−cycle current limiting with a selectable time delayed latched shutdown mode, in-built thermal shutdown, along with a exclusive fault output that will conveniently be interfaced to a microprocessor controller.
Standard motor control attributes incorporate open loop speed control, forward or reverse rotation, run enable, and dynamic braking. On top of that, the MC33035 has a 60°/120° select pin which configures the rotor situation decoder for either 60° or 120° sensor electrical phasing inputs.
PIN OUT Functions:
Pin1, 2, 24 (Bt, At, Ct) = These are the three upper drive outputs of the IC specified to operate the externally configured power devices such as BJTs. These pinouts are internally configured as open collector mode.
Pin#3 (Fwd, Rev) = This pinout is intended to be used for controlling the direction of the motor rotation.
Pin#4, 5, 6 (Sa, Sb, Sc) = These are 3 sensor outputs of the IC assigned to command the control sequence of the motor.
Pin#7 (Output Enable) = This pin of the IC is assigned to enable the motor operation as long as a high logic is maintained here, while a low logic is for enabling a coasting of the motor.
Pin#8 ( Reference Output) = This pin is enabled with a supply current for charging the oscillator timing capacitor Ct as well as provide a reference level for the error amplifier. It can be also used for providing supply power to the motor Hall effect sensor ICs.
Pin#9 (Current Sense non-inverting Input): The signal output of 100mV may be achieved from this pinout with reference to pin#15 and is used for cancelling the output switch conduction during a specified oscillator cycle. This pinout normally links up with the upper side of the current sensing resistor.
Pin#10 (Oscillator): This pinout determines the oscillator frequency for the IC with the help of the RC network Rt, and Ct.
Pin#11 (Error amp non-inverting Input): This pinout is used with the speed control potentiometer.
Pin#12 (Error amp inverting Input): This pin is internally hooked up with the above mentioned error amp output for enabling the open loop applications.
Pin#13 (Error amp output/PWM Input): The function of this pinout is to provide compensation during closed loop applications.
Pin#14 (Fault Output): This fault indicator output may become an active logic low during a few critical conditions such as: Invalid Input code for the sensor, Enable pinout fed with a zero logic, Current sense input pinout getting higher than 100mV (@ pin9 with reference to pin15), triggering of the under voltage lockout, or a thermal shutdown situation).
Pin#15 (Current sense inverting input): This pin is set for providing the reference level for the internal 100mV threshold, and may be seen connected with the lower side current sense resistor.
Pin#16 (GND): This is the ground pin of the IC and is designated to provide the ground signal to the control circuit and is required to be referenced back to the power source ground.
Pin#17: (Vcc): This is the supply positive pin specified to the provide the positive voltage to the control circuit of the IC. The minimum range of operation of this pin being 10V and the max at 30V.
Pin#18 (Vc): This pinout sets the high state (Voh) for the lower drive outputs through the power attributed to this pin. The stage works with the range of 10 to 30V.
Pin#19, 20, 21 (Cb, Bb, Ab): These three pinouts are internally arranged in the form of totem pole outputs and are assigned to drive the lower drive output power devices.
Pin#22 (60 D, 120D phase shift select): The status attributed to this pinout configures the control circuit operation with the Hall effect sensors for either a 60 degrees (high logic) or 120 degrees (low logic) phase angle inputs.
Pin#23 (Brake): A logic low at this pinout will allow the BLDC motor to run smoothly while a logic high will instantly stop the motor operation through a rapid deceleration.
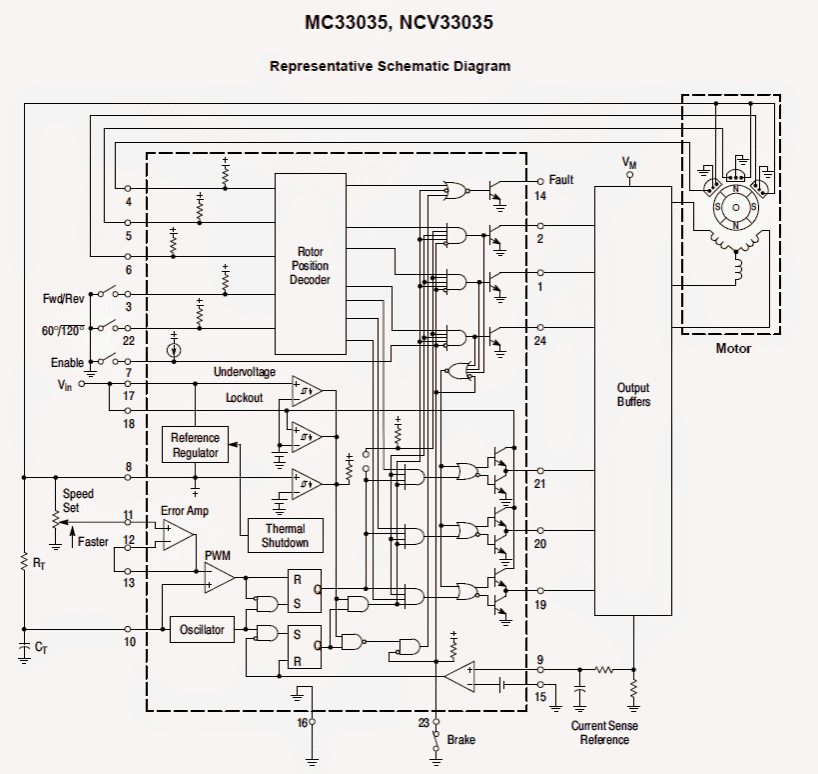
FUNCTIONAL DESCRIPTION
A representative internal block diagram is demonstrated in the above figure. A discourse of the benefits and working of each one of the central blocks enumerated below.
Rotor Position Decoder
An inner rotor position decoder meters the 3 sensor inputs (Pins 4, 5, 6) to render the the right sequencing of the upper and lower drive pinouts. The sensor inputs are manufactured to interface straight with open collector type Hall Effect switches or opto slotted couplers.
In-built pull−up resistors are classified to curtail the necessary amount of external parts. The inputs are TTL compatible, with their thresholds characteristically at 2.2 V.
The MC33035 range of ICs is intended to control 3 phase motors and run with 4 of the most popular conventions of sensor phasing. A 60°/120° Select (Pin 22) is expediently supplied and furnishes the MC33035 to configure on its own to regulate motors having either 60°, 120°, 240° or 300° electrical sensor phasing.
With 3 sensor inputs you will discover 8 potential input code formations, 6 of which are legitimate rotor placements.
The other two codes are outdated as they are generally a result of an open or shorted sensor connection.
With 6 justifiable input codes, the decoder may possibly take care of the motor rotor position to within a spectrum of 60 electrical degrees.
The Forward/Reverse input (Pin 3) is used as a tool to modify the course of motor schedule by reversing the voltage across the stator winding.
As soon as the input alters state, from high to low using a assigned sensor input program code (for instance 100), the facilitated top and base drive outputs using the same alpha status are swapped (AT to AB, BT to BB, CT to CB).
Essentially, the changeable string is changed direction and the motor reverses directional sequence. Motor on/off control is achieved by the Output Enable (Pin 7).
Whenever left disconnected, an internal 25 μA current supply permits sequencing of the leading and base drive outputs. When grounded, the top part drive outputs switch off and the base drives are pushed to low, evoking the motor to coast and the Fault output to trigger.
Dynamic motor braking makes it possible for a surplus margin of protection to be developed into the final device. Braking system is achieved by putting your Brake Input (Pin 23) within a higher status.
This leads to the top drive outputs to switch off and the underside drives to activate, shorting the motor−generated again EMF. The brake input possesses absolute, wholehearted consideration over all other inputs. The inner 40 kΩ pull−up resistor streeamlines interfacing using the program safety−switch by guaranteeing brake activation in case opened up or shut off.
The commutation logic truth table is shown in below. A 4 input NOR gate is employed to examine the brake input and the inputs to the 3 top drive output BJTs.

The objective is usually to turn off braking before the top drive outputs accomplish a high status. This allows you to avoid synchronized leasing of the the top and base power switches.
In half wave motor drive programs, the top drive components are generally not needed and they are in most cases kept detached. With these types of circumstances braking is still going to be attained because the NOR gate detects the base voltage to the top drive output BJTs.
Error-Amplifier
An improved efficiency, fully compensated error amplifier with active access to each inputs and output (Pins#11, 12, 13) is offered to assist in the execution of closed-loop-motor speed control.
The amplifier comes with a standard DC voltage gain of 80 dB, 0.6 MHz gain bandwidth, along with a wide input common mode voltage range that stretches from ground to Vref.
In the majority of open loop speed control programs, the amplifier is set up as a unity gain voltage follower with the noninverting input coupled to the speed set voltage supply.
Oscillator The frequency of the inner ramp oscillator is hard-wired through the values decided on for timing elements RT and CT.
Capacitor CT will be charged through the Reference Output (Pin 8) by means of resistor RT and discharged through an inner discharge transistor.
The ramp peak and pit voltages are normally 4.1 V and 1.5 V correspondingly. To offer a decent skimp on among audible noise and output switching performance, an oscillator frequency in the selection of 20 to 30 kHz is suggested. Make reference to Figure 1 for component selection.
Pulse Width Modulator
The integrated pulse-width-modulation offers an power effective approach to governing the motor speed by altering the standard voltage ascribed to every stator winding throughout the commutation series.
As CT discharges, the oscillator models each latches, enabling conduction of the uppper and lower drive outputs. The PWM comparator resets the top latch, terminating the lower drive output leasing once the positive−going ramp of CT turns into in excess of the error amplifier outcome.
The pulse-width-modulator timing diagram is demonstrated in Figure 21.
Pulse width modulation for speed management presents itself exclusively at the lower drive outputs. Current Limit Constant functioning of a motor that may be significantly over−loaded leads to overheating and inevitable malfunction.
This detrimental situation can easily best be averted together with the use of cycle−by−cycle current restriction.
That is, every on−cycle is dealt with as being a independent function. Cycle−by−cycle current restriction is achieved by tracking the stator current build−up everytime an output switch triggers, and after sensing a high current situation, instantly disabling the switch and retaining it off for the outstanding period of oscillator ramp−up interval.
The stator current is transformed into a voltage through applying a ground−referenced sensing resistor RS (Figure 36) in line with the 3 lower part switch transistors (Q4, Q5, Q6).
The voltage established along the anticipating resistor is supervised with the Current Sense Input (Pins 9 and 15), and compared with the inner 100 mV reference point.
The current sense comparator inputs come with an input common mode range of roughly 3.0 V.
In the event the 100 mV current sense tolerance is surpassed, the comparator resets the lower sense lock and ends output switch conduction. The value for the current sensing resistor is actually:
Rs = 0.1/Istator(max)
The Fault output initiates while in an high amp situation. The dual−latch PWM setting makes certain that just one single output trigger pulse arises in the course of a certain oscillator routine, whether or not ended by way of the output of the error amplifier or the current limit comparator.
The on−chip 6.25 V regulator (Pin 8) offers charging current for the oscillator timing capacitor, a reference point for the error amplifier, which enable it to supply 20 mA of current appropriate for specifically powering sensors in low voltage programs.
In larger voltage purposes, this could grow to be important to exchange the power emitted from the regulator off the IC. This is definitely achieved with the help of another pass transistor as demonstrated in Figure 22.
A 6.25 V benchmark point seemed to be decided to enable rendering of the straightforward NPN circuit, wheresoever Vref − VBE surpasses the minimal voltage essential by Hall Effect sensors over heat.
Having proper transistor assortment and sufficient heatsinking, as much as 1 amp of load current can be purchased.
Undervoltage-Lockout
A three-way Undervoltage Lockout have been integrated to reduce harm to the IC and the alternative power switch transistors. During low power supply factors, it ensures the fact that IC and sensors are completely functional, and that there is adequate base drive output voltage.
The positive power supplies to the IC (VCC) and the low drives (VC) are each examined by independent comparators that get their thresholds at 9.1 V. This particular stage guarantees adequate gate commute required to attain low RDS(on) whenever driving ordinary power MOSFET equipment.
Whenever directly energizing the Hall sensors from the reference, inappropriate sensor operation appear in the event the reference point output voltage drops underneath 4.5 V.
A 3rd comparator can be used to recognize this issue.
When more than one of the comparators picks up an undervoltage situation, the Fault Output is turned on, the top runs are put off and the base drive outputs are organised in a low point out.
Each one of the comparators incorporate hysteresis to protect against amplitudes when bridging their individual thresholds.
Fault Output
The open collector Fault Output (Pin 14) had been intended to offer analysis details in case of a process breakdown. It has a sink current ability of 16 mA and may specifically drive a light emitting diode for visible signal. Furthermore, it is actually conveniently interfaced with TTL/CMOS logic for use in a microprocessor governed program.
The Fault Output is effective low while more than one of the subsequent situations take place:
1) Invalid Sensor Input codes
2) Output Enable at logic [0]
3) Current Sense Input more than 100 mV
4) Undervoltage Lockout, activation of 1 or higher of the comparators
5) Heat Shutdown, optimum junction temp getting maxed This exclusive output may also be used to tell apart between motor start−up or endured functioning within an inundated situation.
With the help of an RC network amongst the Fault Output and the enable input, this means you can develop a time−delayed latched shutdown with regard to overcurrent.
Additional circuitry displayed in Figure 23 helps make effortless starting up of motor systems that are fitted with higher inertial loads by giving supplemental pick-up torque, whilst still safe guarding overcurrent protection. This task is achieved by placing the current restrict to the next than minimal value for a established period. In the course of an exceedingly lengthy overcurrent situation, capacitor CDLY will charge, evoking the enable input to get across its tolerance to a low condition.
A latch can now be shaped by the positive feedback cycle from the Fault Output to the Output Enable. When set, by the Current Sense Input, it could only be reset by shorting CDLY or cycling the power supplies.
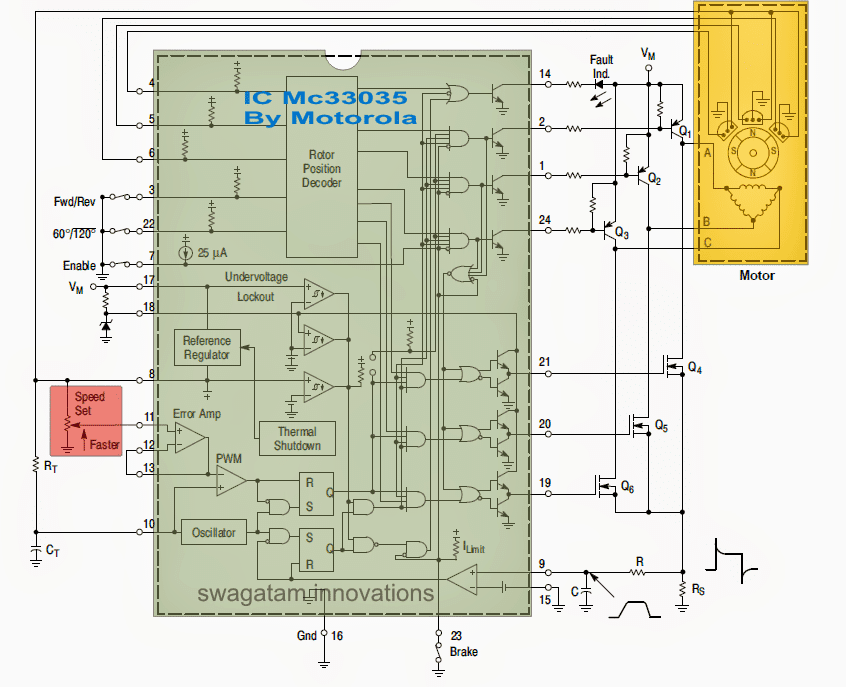
Fully Functional High Wattage BLDC Schematic
A Fully functional high wattage, high current BLDC controller circuit using the above explained device can eb witnessed below, it's configured as a full-wave, 3-phase, 6-step mode:
Hello, my fault output has activated, and I don’t know how to reset it. The datasheet says that I can either short the capacitor Cdly or power cycle the supplies; can you explain how?
You will have to add the CDLY and RDLY components to the circuit. Please refer to the datasheet and try to find CDLY by pressing Cntrl+F in the diagrams, you will be able to locate the CDLY. Power cycling might refer to switching OFF and switching ON the power supply.
Power cycling the supply” typically refers to the act of turning off the power to an electronic device or system, and then immediately turning it back on.
Hello. Can we run a 60V 3000W motor with the diagram above. What can be the switching elements to start a motor with this feature. Thanks in advance for your help
Hello, I don’t think a 60 V supply would work with the above circuit….the maximum is 48 V.
Hi, could you help me? I’m having a problem with the engine starting, it always starts too fast. Once started the speed control is smooth.s
Hi, which engine are you referring to?
I am trying to avoid using figure 25 with boost V schematic figure 30 outlined on the datasheet.
With the availability of high amp darlingtons, can we not just plug-in those components into the schematic?
Please see linked sketch:
https://gentcomponents.com/homeMadeCircuit/toSwag.pdf
Thank you in advance.
Reference: https://www.homemade-circuits.com/400v-40a-darlington-power-transistor-datasheet-specifications/
Yes that maybe possible however the Darlington transistors must be PNP type, NPN will not work.
Thank you for your prompt response.
I am confused. Page 14 of the datasheet says:
“The three top drive outputs (Pins 1, 2, 24) are open collector NPN transistors capable of sinking 50 mA with a minimum breakdown of 30 V”
Can you clarify? PNP in the volt/amp combination needed (20A at +330V) appear to not exist
Again, I’m not opposed to converting the high side to n-channel mosfets per figure 25 and figure 30, but the complexity of the circuit increases.
Because the internal top drive outputs are open collector NPN, they will be compatible with PNP devices at the output for the high side devices….if you use NPN transistors at the high side, they will start behaving like inverters which would be incorrect, that is why we need PNP devices on the high side so that they switch ON simultaneously when the top NPN drive transistors switch ON.
You can use MJE5852 which are 400V 8 amp transistors, you can connect 3 of them in parallel on each group
Hello Swagatam,
I’m a mechanic who know nothing about electronics. i’d like to build a 3ph bldc motor from an old 125cc cub’s alternator / PMG (sensorless if possible). can this controller be used for it? would you mention all the value of each electronic component that used? Thank you
Hello Budsis, I am afraid the above circuit is strictly suitable only for the experts, and I cannot recommend this circuit for anybody who is extremely new to electronics. I would rather suggest you to buy a ready-made BLDC driver module for your purpose.
There are many aspects in the circuit that will need to be calculated as given in the following datasheet
https://www.onsemi.com/pdf/datasheet/mc33035-d.pdf
Would you specify the value of each component of the circuit diagram you made? I’ll ask my friend to help me assemble it for me.
Please specify the voltage and current of the motor.
Thank you very much for your valuable time.
Sir, I have make a 3 phase bldc motor that contains 9 slot stator.but I have two permanent magnet rotor, 6 pole and 8 pole.which one be use for more power and effiency ?
Soumen, 8 pole will give more power, however 6 pole will be also fine…
Dear admin,
With due respect
I have some question from above circuit diagram
1: can i use irf4905 or irf9540n p-ch mosfet instead of tip147 pnp transistor ?
2: which is suitable for better performence,BJT or mosfet ?
3: can i load a 24v 500w bldc motor in this circuit ?
Thank you a lot for your time and kind regurds.
Dear Somen,
MOSFETs gates cannot work above 15V, so you can add zener diodes across the gate/source of the p channel MOSFeTs, and then probably it may work….
FETs are better than BJTs in high power switching application circuits
You can load any type BLDC motor with the last circuit
Hello Swagatam
I got the wiring specs from BOMA factory, as follows:
The motor has 9 coils spaced 40 degrees each and wired in three phase scheme, each phase having three coils in series. Wires are coloured blue green yellow and provided with 2.5 mm2 gauge cables.
It has also three Hall sensors, installed in consecutive coils, each spaced 40 degrees. Are wired with three thin cables having the same color code of blue green yellow for sensor identifying.
Two more thin wires coloured black and red are provided to energize and ground the Hall sensors.
Finally, the permanent magnet rotor has six poles.
Do you think that this BOMA motor (48 V, 1000 Watt, 2800 RPM) is suitable to be driven with your 33035 based circuit ?
If you think it is I go ahead,
If not, can you suggest another option ?
Thanks so much for your time, and kind regards
Horacio
Hello Horacio, I thin we can ignore the black, red thin wires for the moment, and try configuring the remaining useful wires with the above circuit or any similar BLDC driver circuit that involves 3 input from the hall sensors.
So you can definitely try the above circuit design for the specified BOMA 48 V motor, which probably looks quite compatible with your motor specs.
Hello Swagatam
I will go with this option.
I have two pics of my motor opened, so you can see exactly what are we talking about.
I have also asked the provider for a schematic of the color cables, the three main wires are green blue yellow, but I dont know if there is a standard to identify RST
The five yhin cables are black, green, yellow, red, blue. Normally 4 of them are Hall sensors, with one common for the three sensors, and one for each sensor line.
The fifth one I have no idea.
I hope the factory will provide a correct schematic diagram.
On my side, I see that I must select the three darlingtons and the three MosFets.
Can you guide me with that ?
Finally, where can I send you the two pictures ?
Kind regards,
Thank you very much,
Horacio
Hi Horacio, Actually seeing the motor images might not provide any helpful information, unless a proper wiring diagram is available, so I think we will have to wait until the correct schematic diagram is acquired from the manufacturer.
Yes the last diagram is the one you will have to build for implementing the motor control. The high side transistor can be any power BJT such as TIP36, and lower side FETs can be IRF540
Sir can you please help me with a circuit based on this design.
https://drive.google.com/file/d/1E6RDlKcaDARFKbrh8_Gq-8kl9BEVB1CL/view?usp=sharing
Sorry Marvin, I am not familiar with the working specs of this IC, so at this moment it may not be possible for me to analyze the design.
Sir, I saw this 200amps DC motor controller circiut online which had a 200amps current sensor (acs758).Due to my curiosity I built a replica of the circuit and connect it to five 200amp 200volt n-channel mosfet but the fault led on .Do you think this circuit is going to work or do you have a circuit similar to this design based on mc33035. https://drive.google.com/file/d/0B8lWCxw9fOK8c3RhcnRlcl9maWxl/view?usp=sharing
Marvin, there’s no schematic in the link.
hello sir,
i also want to confirm if its possible to neglect the Hall sensor.
Hello Basit, for sensorless design you can refer to the following concept
https://www.homemade-circuits.com/high-current-sensorless-bldc-motor/
Hello sir,
It’s been a while sir, I just want to confirm if I can use 3205 fet on this circuit sir(33035p). I want to use it to drive a 3phase bldc water pump(cwa 200) sir.
Hello Basit, sorry I am not so sure if MOSFEts can be used at the output in the usual manner, because modifying the manufacturers design can be risky.
Hi sir,
I planning to design a bldc senserless controller I have 2000w bldc motor for my cycle . I was Google lot I didn’t get any circuit diagram plz help me to make a esc controller share me your great knowledge plz
You can try the following concept, by replacing the MOSFETs appropriately
https://www.homemade-circuits.com/high-current-sensorless-bldc-motor/
Kako povezati IBT-2 arduino sa arduino uno ikako napisati kod za DC motor brisaca.?
pozdrav!!
sorry I have no idea about it
sir abioye just resend the mail with my email address he claimed that he sent the first one to a wrong email address i will look forward to your reply sir
Marvin, I prefer discussing through comments only on this platform, but anyway I’ll check it this time.
dear sir,
can i replace/use tip35c and tip36c instead of irf540n and tip147 ?
please tell me what will happen with motor power and effiency?
Hello Soumen, No that won’t work according to me….MOSFETS cannot be replaced with BJTs here!
sorry sir my friend abioye sent an email to you sir on my behalve with his email (abbyadewale4@gmail.com) thanks sir
I checked, nothing found with that email, even in my spam box
sir i sent you an email with picture of igbt gate driver i made with discrete transistor i will be forever grateful if you answer my request sir because it been weeks know that have been battling with it i have not yet test it because am not sure of myself and i dont want to damage the expensive igbt i just bought, and am very sure sir that you could find a solution to my problem sir
Marvin, sorry I couldn’t find any related email in my email ID. You can save the diagram in your Google drive and send the link here, I’ll check it out. Make sure the image can be viewed by all, and is not private.
sir assuming 0.1 ohm give 1volt to pin (9) non inverting input of mc33035 to allows 7amps to pass to the motor what if i wire (243) 0.1 ohm in series to generate 1volt for the mc33035 at the non inverting pin (9) to allow 1700 amps to get to a DC motor.
And sir one of my friend said a IGBT can be use as a freewheeling diod if the gate of a IGBT is shorted to the emitter is it true sir
you have to put the resistors in parallel. and make sure the leads are small, and also the other connections to this network are done with very thick copper wires.
yes that’s possible but I have not yet tested or used transistors as diodes
sir i divide 0.1 by 1700amps and i get 0.0000588235 as the value of resistor sir what ohm or watt do i have to use sir, because i have a mc33035 circuit to control two brushed dc motor with big igbt
And sir for some time now i have been curious about something , if i have 300volt 3000amps battery and i bought a 600volt 1200amps dc controller will the high amperage battery damage the controller or the 1200amps is the maximum amps the controller can supply the motor
thank for always been there for me sir i am very grateful sir
abioye, that value seems impractical, it is better to use a power supply whose output may be matching the motor specs.
the 600V controller will get damaged only if the rated 600V is exceeded at the input.
The controller will be able to supply only the specified 1200 amp max, and may get damaged if this value is exceeded, unless it is overload protected internally
sir what does the( istatormax) represent in the formula to calculate the amount of amps or is it (0.1/motor maximum amps)
Abioye, that is the max stator current, or the motor current specification.
What is the max voltage and amps that this can handle?
I’m wondering if this is a good use for my 600v 600a IGBT’s and a 120v battery pack.
Max voltage is 48V, The current can be as per your load specifications, at any level, You can refer to the last diagram where the output devices can be appropriately tweaked for obtaining the desired amount of current for the motor…
Good day Swagatam…Do you have a simple circuit to control the speed of ac motors just like a variable frequency drive motors. Thanks…
Good-day, you can use the concept which is explained in the following article, but it won't work like VFD rather will do it by phase chopping
https://www.homemade-circuits.com/2012/03/how-to-make-25-amp-1500-watts-heater.html
you can try replacing the heater with your motor
Sir, IC 33035 comes in two variants MC33035DWG and MC33035DW2RG, What is the vmeaning of this DW and DW2RG ?
Dev, you will have to check and compare the datasheets of the two….most probably the initial section of the datasheet will tell you the difference between the two….
Swagatam ji, can you ref a circuit for running a 12 V High Current BLDC motor… will the circuit given by you (below link) handle such high current since mosfet is isolated form the IC circuit,
https://www.homemade-circuits.com/2014/12/simple-3-phase-brushless-bldc-motor.html
Pranavji, the linked circuit will be able to handle any amount of specified current if the IGBTs are appropriately rated for handling it.
Thank you ji, i shall try and if able to successfully run a BLDC motor shall share the details on this page.
will it be possible to create a circuit with a back EMF instead of hall effect sensor.
OK thanks,
according to me the hall effect sensors are the integral part of most BLDC motors, that cannot be changed.
Pls sir i'm very very sorry to disturb you again but i want you to help me with the wattage and resistance of the resistors that i will connect to the base and enmiter of the transistor so that i'll get 5amp at the output of the link you directed me to.
which link? …please provide it.