In this post we try to understand the method of dimensioning or calculating inductors in buck boost converter circuits in order to ensure an optimal performance from these devices.
We take the example of IC 555 boost converter and IC 555 buck converter typologies, and try to understand the optimizing techniques through equations and manual adjustments, for achieving the most optimal output response from these converter designs.
In a few of my earlier posts we comprehensively studied regarding how SMPS buck and boost converters work, and we also deduced a few fundamental formulas for evaluating the important parameters like voltage, current and inductance in these converter circuits.
You may want to summarize the details from the following articles, before embarking on the present article which deals with the inductor designing methods.
Basic Buck Boost Equations
For calculating inductors in buck boost SMPS circuits, we could derive the following two concluding formulas for a buck converter and for a boost converter respectively:
Vo = DVin ---------- For Buck Converter
Vo = Vin / (1 – D) ---------- For Boost Converter
Here D = Duty Cycle, which is = Transistor ON time / ON + OFF time of each PWM cycle
Vo = Output Voltage from the converter
Vin = Input supply voltage to the converter
From the above derived formulas, we can understand that the 3 basic parameters which can be used for dimensioning the output in an SMPS based circuit are:
Main Parameters Associated with Buck Boost Converter
1) The Duty cycle
2) The Transistor ON/OFF time
3) And the Input Voltage level.
This implies that by appropriately adjusting any one of the above parameters it becomes possible to tailor the output voltage from the converter. This adjustment could be implemented manually or automatically through a self adjusting PWM circuit.
Although the above formulas clearly explain how to optimize the output voltage from a buck or boost converter, we still do not know how the inductor can be built for getting an optimal response in these circuits.
You may find many elaborate and researched formulas for settling this issue, however no new hobbyist or any electronic enthusiast would be interested to actually struggle with these complex formulas for the required values, which could actually have more possibility of providing erroneous results due to their complexities.
The better and more effective idea is to "calculate" the inductor value with an experimental set up and through some practical trial and error process as explained in the following paragraphs.
Configure a Boost Converter Using IC 555
A simple IC 555 based boost and buck converter designs are shown below which could be used for determining the best possible inductor value for a particular SMPS boost converter circuit.
The inductor L may be initially made arbitrarily.
The rule of the thumb is to use the number of turns slightly higher than the supply voltage, therefore if the supply voltage is 12V, the number of turns could be around 15 turns.
- It must be wound over a suitable ferrite core, that could be a ferrite ring or a ferrite rod, or over an EE core assembly.
- The thickness of the wire is determined by the amp requirement which initially won't be a relevant parameter, therefore any relatively thin copper enameled wire would work, may be around 25 SWG.
- Later on as per the current specs of the intended design, more number of wires could be added in parallel to the inductor while winding it in order to make it compatible with the specified ampere rating.
- The diameter of the inductor will depend on the frequency, higher frequency would allow smaller diameters and vice versa. To be more precise, the inductance offered by the inductor becomes higher as frequency is increased, therefore this parameter will need to be confirmed through a separate test using the same IC 555 set up.
Circuit Diagram Boost Converter
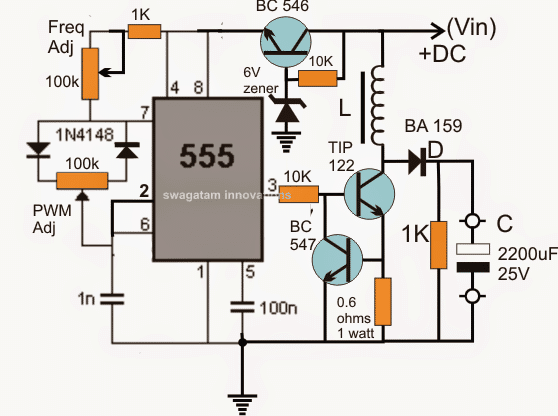
Optimizing the Potentiometer Controls
The above set up shows a basic IC 555 PWM circuit, which is equipped with separate potentiometers for enabling an adjustable frequency, and an adjustable PWM output at its pin#3.
Pin#3 can be seen connected to a standard boost converter configuration using the TIP122 transistor the inductor L, the diode BA159 and a capacitor C.
The transistor BC547 is introduced to limit the current across the TIP122 so that during the adjustment process when the pots are being tweaked the TIP122 is never allowed to cross the breakdown point, thus the BC547 safeguards the TIP122 from excessive current and makes the procedure safe and foolproof for the user.
The output voltage or the boost voltage is monitored across C for a maximum optimal response during the entire testing process.
The IC 555 boost converter could be then manually optimized through the following steps:
- Initially, set the PWM pot to produce the narrowest possible PWM at pin#3, and the frequency is adjusted to about 20kHz.
- Take a digital multimeter fixed over above 100 V DC range and connect the prods across C with appropriate polarity.
- Next, gradually adjust the PWM pot and monitor as long as the voltage across C continues to rise. The moment you find this voltage dropping, restore the adjustment to the previous position which yielded the highest possible voltage on the pot, and fix this pot/preset position as the optimal point for the selected inductor.
- After this, tweak the frequency pot similarly for further optimization of the voltage level across C, and set it to achieve the most effective frequency point, for the selected inductor.
- For determining the duty cycle one could possibly check the PWM pot resistance ratio, which would be directly proportional to the mark space ratio of the pin#3 output duty cycle.
- The frequency value could be learned through a frequency meter or by using the frequency range across the given DMM if it has the facility, this could be checked at pin#3 of the IC.
Your inductor parameters are now determined and could be used for any boost converter for the best optimal response.
Determining Current for the Inductor
The current spec of the inductor could be increased by simply using many parallel wires while winding it, say for example you could use around 5 nos of 26SWG wires in parallel for empowering the inductor to handle 5amps of current. and so on.
The next diagram shows the process of optimizing and calculating inductors in SMPS, for a buck converter application.
Circuit Diagram Buck Converter
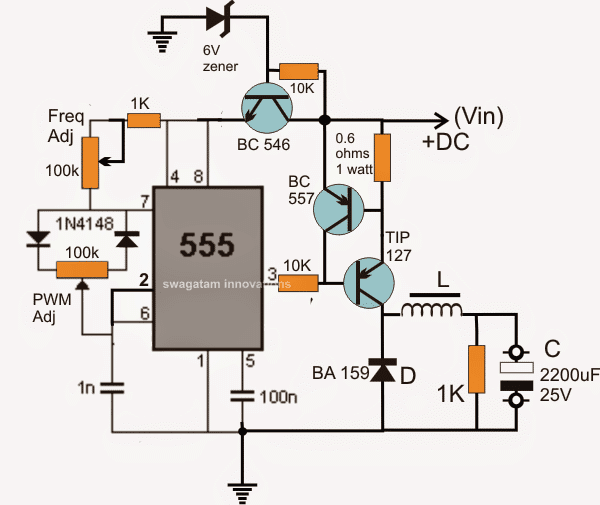
The same process applies for this set up too, as was done with the above explained boost converter design.
As can be seen the output stage is now altered with a buck converter set up, the transistors are now replaced with PNP types and the positions of the inductor, diode changed appropriately.
Thus, by using the above two methods anybody can determine or calculate inductors in buck boost smps circuits without using complex and unfeasible formulas.
Sanjay says
Hi Sir
I need a buck circuit with wide input voltage from 10 to 120 volts and output of 14volts 10 amps. Request your help with the circuit and Inductor value and capacitor value and switching frequency
Swagatam says
Hi Sanjay,
120V is too high, I have a circuit which can handle a maximum of 40 V only.
PWM Solar Battery Charger Circuit
Bello says
Dear Mr Swagatam.If I want to increase the amperage (to like 10amps) of this boost converter what do i need to do?
Swagatam says
Dear Bello, current can be increased by increasing the wire thickness or density, but first verify the proper working of the basic design, only then the upgrade can be implemented.
Tolu says
Please what’s the function of bc546 and the zener 6v.thanks
Swagatam says
it is configured as a voltage regulator, for stabilizing the supply to the IC at 6V fixed
Tolu says
Hi Swag, between the bc546 and zener, and 7806 voltage regulator, which is better between the two. Thanks sir
Swagatam says
Hi Tolu, 7806 is better but its input voltage is limited to maximum 32V.
tinuke says
I tried this ic 555 buck converter circuit but the the Vout just had 0.25v diff without no variation despite turning the pwm preset. The gate and emitter voltage are thesame. What can I do .thanks
Swagatam says
that’s not possible unless you have done some mistake in your connections, I will try to upload a working video of it soon…
tinuke says
Thanks Swag, the buck converter worked. But its configuration is different from that one in simple mppt circuit which I tried but not working. Like I said earlier, the p1 resistance variation is range of 0-236ohms. Any advice to that.
Swagatam says
Did you check the procedures which I suggested you earlier by isolating the various stages? disconnect the IC1, IC2 the opamp and the solar panel from each other, confirm the stages separately
tinuke says
I did it, anything less than 10v the ic2 didn’t drive the motor.
Swagatam says
pin#5 of IC 2 is already at 2/3rd Vcc internally, and will able to produce 75% speed on the motor when nothing is applied at pin#5, reducing this level to lower values will proportionately reduce the motor speed…it is a standard IC 555 pwm circuit
you can understand it better by referring to this post
https://www.homemade-circuits.com/constant-torque-dc-motor-speed/
tinuke says
Hello, I changed the tip in the Buck converter to p-channel MOSFET, there was wide variation in the voltage as against the tip with no much difference why varying the pots. Why the transistor not showing difference as to the MOSFET in reference to the Vin.
Swagatam says
If your IC works correctly and if you are able to vary the PWM at pin#3 then definitely you will be able to see a varying output through the buck.
did you test the PWM with an oscilloscope? test it with a scope that will prove whether your circuit is working correctly or not.
tinuke says
Please I need a simple dc-dc converter circuit to step down 48v to 12v for my inverter oscillator stage.
Swagatam says
search for buck converter in this website, you can use it for the purpose…
tinuke says
I tried this ic 555 buck converter circuit but the the Vout just had 0.25v diff without no variation despite turning the pwm preset. The gate and emitter voltage are thesame. What can I do .thanks
charan says
hi, i made the above boost converter circuit for boosting voltage to 5v from a 4v battery. but circuit was boosting upto 50v starting from 12v. so i couldnt get 5v even after trying different inductor combinations and also the calculated duty cycle for my circuit was >20%.
so what might be the solution to get 5v ? also whn i replaced trnsr with fet(irf 540) it was not switching so ive a doubt that whether 540 operates at 4v ?
Swagatam says
Hi, it is possible to reduce the voltage to 5V, you must check by connecting a dummy load of may be a 1K resistor at the output. and then reduce the number of turns to a value which will get you to 5V. You will have to also experiment with the frequency for lowering the voltage and make sure the frequency matches with the coil inductance.
yes a mosfet will not work properly below 8V
rahul says
lm 2596 and transistor—vs—-lm 317 and transistor——-
i am confused which way to go———-
i have heard in many forums—that switching regulators—better voltage regulation—lesser heat dissipation—is it true ?
logic——-suppose output will be 5V x 1A = 5W. If the switcher have 85% efficiency, then the total input power will be 5W / 0.85 = 5,88W. The difference between the output power and the input power is the what we looking for heat dissipated 0,88W.
but lm 317 is (input-output voltage)*current——-so greater amount of heat developed
———but problem in switching regulator—–suppose output is 7 v *6a=42 w—-input-42/.55=76 w ( i am considering efficiency 55 % because input is 60 v output i took is 7 v –step down-as effiency decreases drastically in switching regulator from datasheet)—-so 34 w heat dissipated immidiately lm 2596 will die—-i guess max heat dissipation in switching is 10 w
———so according to you which way to go better ?
—-i dont know how to handle 300 w load with lm 2596–can i put transistor, mosfet or more no lm 2596 ?
Swagatam says
If you can build a switching regulator correctly then you should go for that, and get maximum efficiency. You can refer to this LM317 based switching regulator also:
https://www.homemade-circuits.com/lm317-variable-switch-mode-power-supply/
rahul says
thank you——in my city kolkata—only switching regulator lm 2596 available——
1—–lm 2596 and transistor–npn—-to increase current output more than 3a——is it possible ?
2—-lm 2596—-4—-in parallel ——–is it possible ?
Swagatam says
I don’t think any external modification will work with LM2596, because it is a buck converter design and any modifications across the pinouts may result in malfunctioning of the IC….
rahul says
ok——thanks
kiran says
Sir
What happend when the indectence value is smaller than specifaid indectence of buck convertor . Is it effect the out put voltage of bucknconvertor ?
The indectence value is directly or indirectly propotional to out put voltage of buck convertor .
Swagatam says
Kiran, smaller than the required level will cause heating up of the coil and the driver transistor.
Inductor value in inversely proportional to current output.
naseef says
Sir . I made a buck convertor that drive a high voltage dc to convert 300v dv to 150 v dc . The pwm signal used 31 khz from ardino . But my out put is 28v only . Where is my mistake . ???
Swagatam says
Naseef, the voltage level from a buck converter primarily depends on the number of turns of the coil or the inductance value and the PWM “ON time”…make sure these parameters are correctly calculated for the required 150V output
naseef says
Sir
But my IGBT (25N120) only get 20 to 30 volt on emitter if giving 300v on collector . Inspate of Gate voltage is nearly 10v .
My pwm is 50 % ON time
Swagatam says
naseef, the emitter voltage will be equal to the gate level, therefore the gate should be higher than the required output voltage…in your case it must be 150 + 2V.
configure the IGBT stage as done in this article
https://www.homemade-circuits.com/2015/05/5v-pwm-solar-battery-charger-circuit.html
naseef says
Sir . Eny alternate method for switching my IGBT with low voltage from optocoupler
Swagatam says
naseef, the emitter voltage will be almost equal to the gate voltage, so for example if you feed 2V at gate, the emitter will be also at around this level. I hope you have understood the theory.
Unknown says
Thank u mr swagatam i understand the principle better it is a trial and error thing I will do and let u know sir . Thank u Alex
Swagatam says
sure Mr. Alex, ……it's not quite a trial and error method, because here you are able to monitor the results while optimizing it.
naseef says
Thanks sir . I understand .