6 Simple AC Bridge Circuits Explained

An AC bridge is a circuit which can be used for measuring parameters like capacitance, resistance, Inductance using differential method, by comparing them with known values of similar components, positioned diagonally across a bridge circuit, and through an analogue meter placed at the center of the bridge.

Before we begin talking about the AC bridge circuits using capacitance and/or inductance, it may be important to understand several related terminologies. The capacitors and inductors that are ideally suited for the application are specified with reactance in an AC circuit, instead of resistance.

Important Parameters

Reactance represents the AC variant of "resistance," which is indicated in ohms. Impedance is one more relative term which is utilized to express the whole combined result of reactance and resistance in certain section of a circuit, and is indicated in ohms.

In the practical world capacitors and inductors both may consists of resistance and reactance, therefore while talking about them we imagine them also having an impedance and not just only reactance.

Since the AC bridge circuit legs might consist of both reactances and/or resistances, we'll discuss these legs of the bridge with regard to impedance and not resistance.

To be precise , resistance and impedance can be incredibly identical. The factors for keeping an AC bridge balanced are exactly the same as a DC bridge, we only insert an impedance (symbolized as Z) instead of the resistance.

This provides us with extremely standard equations which can be used with any relevant circuit.

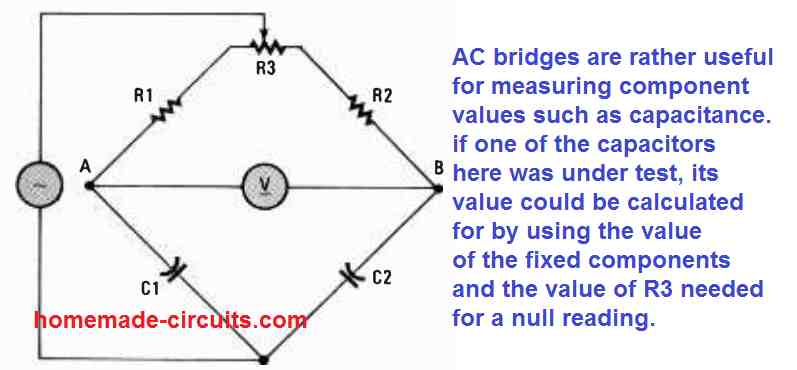
AC bridges work quite well for calculating component values, for example the capacitance. In case we had a capacitor here under test in an AC bridge circuit, its value could be determined utilizing the values of the components in the bridge whose values are known, along with the value of R3 which may be necessary for implementing the null reading.

1) Measuring Small Capacitance Differences

In case we want to determine small differences in capacitance of a capacitor, we could start using an AC bridge circuit like the one shown in Fig. 1 below. Considering that a resistor's impedance is strictly resistive and a capacitor's impedance is practically completely reactive, the impedance of the upper branches of the bridge simply cannot can be different to the lower branches.

In this circuit R1/C1 = R2/C2 when the R3 is correctly adjusted for getting a zero or null reading on the voltmeter V.

This indicates that the second set of conditions needed for balancing (ZA = Z3 and Z4 = ZB) cannot be be fulfilled. The third conditions required for balance the AC circuit cannot be fulfilled either.

Having said that, we can see that the initial conditions (ZA = ZB and Z3 = Z4) could be fulfilled. The impedance ZA consists of R1 and a part of R3, while the impedance ZB comprises of R2 and a some part of R3. The impedance Z3 is attributed to the capacitor C1, while Z4 is the impedance that is used to represent C2.

Provided that C1 remains equal to C2 and any R1 and R2 difference is tweaked and corrected by R3, then we can achieve a well balanced bridge.

Here the impedance of active components, such as resistors and capacitors is determined by the frequency. However we find that the Fig. 1 is not dependent on frequency because the C1, C2 reactances could alter together whenever the frequency changes.

An additional variant of the above discussed AC bridge circuit can be seen in Fig. 2. Although this circuit is designed to work well, it isn't one of the favorite AC bridge versions due to the presence of the DC isolation across only one side of the meter (at point B).

In this circuit R1/R2 = C1/C2 when the variable resistor R3 is appropriately adjusted to get a zero or null reading on the meter V.

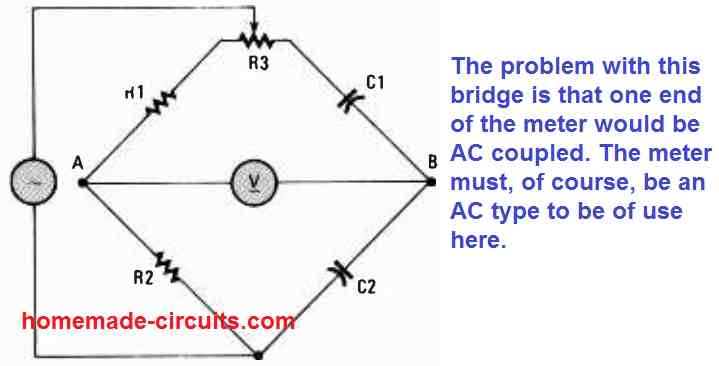
If a DC content comes through the input source, it could result in much unfavorable effects. Additionally it could be complicated to bias a meter-input amplifier hooked up at point A without modifying the input signal level at A.

2) Using Only Capacitors

It is possible to create an AC bridge circuit using only capacitors as demonstrated in Fig. 3 below.

In this circuit, C1/C2 = C2/C4, when the variable resistor R1 is carefully adjusted until a zero or null reading is obtained on the meter V

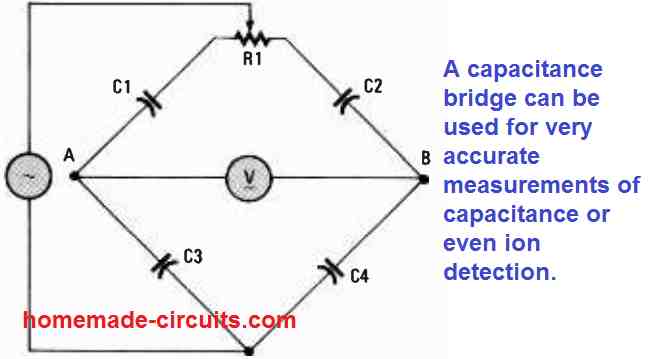
Let's analyze the initial condition (ZA = ZB and Z3 = Z4). Given that the reactance of the capacitor pairs C1/C2 and C3/C4 can change in the same way in response to the changing frequency, the balanced state of the AC bridge is not dependent on the frequency.

This is likewise true for the 3rd condition (ZA = ZB = Z3 = Z4). Another alternative could be that C1 and C3 are made identical, and C2 and C4 are made identical. With these conditions fulfilled and the input frequency fine-tuned to get identical phase shift across points A and B, a perefct balance can be achieved in the bridge circuit.

However, the above conditions prevents the bridge from being independent to the input frequency. Regardless of what conditions we use for getting the AC bridge circuit properly balanced, if the value of any one of the capacitors is changed will cause the generation of an AC voltage output between points A and B.

Since the points A and B are both kept well isolated from the input AC power source, it is fairly easy to connect this high impedance points to any preferred differential amplifier for further processing of the results.

3) Using Inductance and Capacitance Together

Inductors and capacitors both could be applied in an AC bridge circuit, as indicated in Fig. 4.

In this network, L1/R2 = R1/C1, when R3 is perfectly adjusted to bring a zero or null on the meter V.

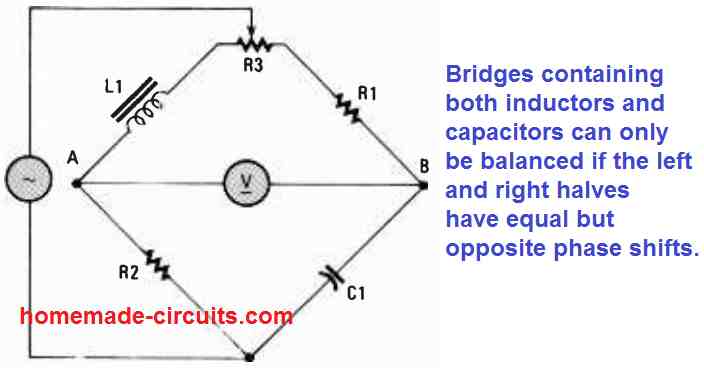
So far, the phase shift symbols of active components did not demand consideration. However, inductors and capacitors both can give rise to phase shift. Capacitors possess a positive phase shift, and inductors can generate negative phase shift. Therefore, in case an inductor is connected in one leg of the of the AC bridge, a capacitor must be connected at the other opposite leg (unless you may want to work with an additional inductor hooked up at the adjacent leg of the AC bridge). These elements will possess equal and opposite phase shift only when they are positioned diagonally across from one another in the AC bridge diagram.

However , the phase shift needs to be identical for the left-hand and the right-hand portions of the circuit together. This may be only achievable at frequency levels where the reactances of the active components are identical. Therefore, the L1 and C1 reactances in Fig. 6 should be identical to one another at the operating frequency.

It is possible to balance the shown bridge if an additional condition is implemented. The rule is, If the L1 reactance of becomes equal to the R1 resistance, and the C1 reactance becomes same as the the R2 resistance at the operating frequency. This means that R1 should be same as R2.

We can evaluate the reactances of the capacitive and inductive components in an AC bridge circuit by replacing R1 and R2 with variable resistance, or potetiometers. After this we can measure the resistance, once proper balancing of the pots are accomplished.

4) Using Identical Inductances and Identical Capacitances

A much easier method would be to insert identical inductances and identical capacitances in the AC bridge legs as shown in the following Fig. 5 and then balance the bridge circuit by having inductance and capacitance on the other leg within the same bridge.

In this circuit L1/C1 = L2/C2 when R1 is carefully tweaked to get a zero or null reading on the meter V

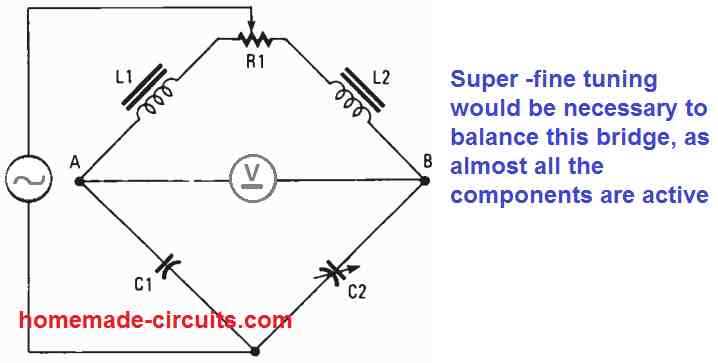
In this AC bridge circuit, the phase shift across the two left and right sections are the same for a particular frequency. A little modification in either the capacitance or inductance within one of the bridge legs will cause the generation of an AC output at points A and B. This bridge circuit could be balanced by fine-tuning C2 instead of a adjusting the resistor for the balancing.

5) Using Only Inductors

An AC bridge circuit using only inductors can be seen in Fig. 6 below.

In this configuration, L1/L3 = L2/L4 when R2 carefully adjusted to get a zero or null reading on the meter. R1 is used for fine tuning and ensure that the meter reading comes perfectly to the zero mark

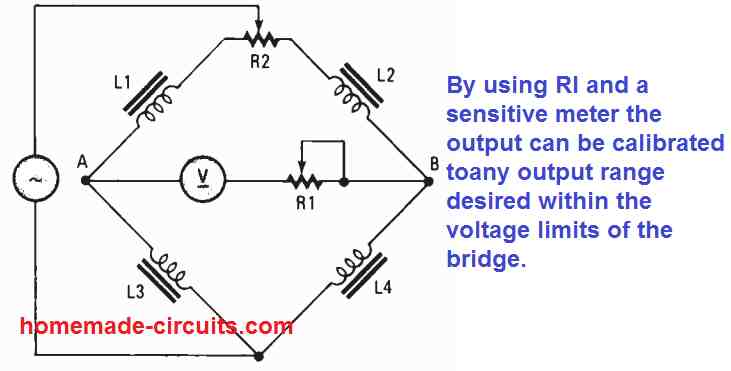
By adding a sensitive voltmeter in series with a variable resistor, it becomes possible to calibrate to any desired output range within bridge's tolerable voltage range. This bridge can perform very nicely for detecting the inductance value of any type of inductor that may be introduced in the bridge.

6) One Bridge Inside Another

There are also AC bridge circuits that include one bridge inside another bridge. Such types of circuit can be used for determining the combined results of more than a couple of versions of the circuit, as indicated in the Fig. 7 below.

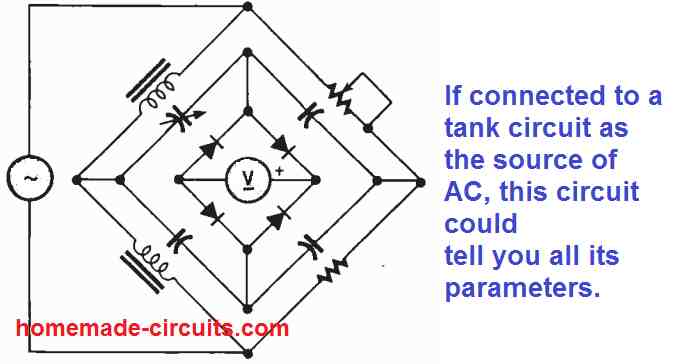
The bridge network which is near the meter works like a full-wave rectifier that let's us know regarding the DC meter's sensitivity for displaying the changes in the AC voltages.

If necessary it may be possible to include more than one element to the specific legs of the bridge.

While this could make the system quite complex mathematically, the factors required for the balance may not change, meaning, to keep identical voltage difference at the nodes while closely watching and adjusting the phase shift. Understanding regarding phase shift and exactly what components need to complement with one another in the AC bridge circuit is really important, if you are intending to utilize the circuits to your greatest advantage. Getting well versed with the fundamentals of the AC bridge circuit could resolve many of your future electronic design complications.