The sinusoidal waveform or sine wave is the most commonly used AC waveform in circuit theory. When a periodic AC waveform is produced by a voltage source, it creates an EMF that changes polarity at regular intervals, with the time it takes to complete one full reversal known as the waveform's period.
Direct current, also known as DC, is a type of electrical current or voltage that flows in one direction around an electrical circuit, making it a "uni-directional" supply.
Power supplies, batteries, dynamos, and solar cells are some of the devices that produce both DC currents and voltages. A DC voltage or current has a fixed amplitude and a definite direction, such as +12V representing 12 volts in the positive direction or -5V representing 5 volts in the negative direction.
DC power supplies maintain a constant value and direction without changing over time, creating a continuous steady-state flow. In other words, a constant uni-directional DC supply will not change or become negative unless its connections are physically reversed. A simple DC or direct current circuit is shown in the example below.
Waveform in a DC Circuit
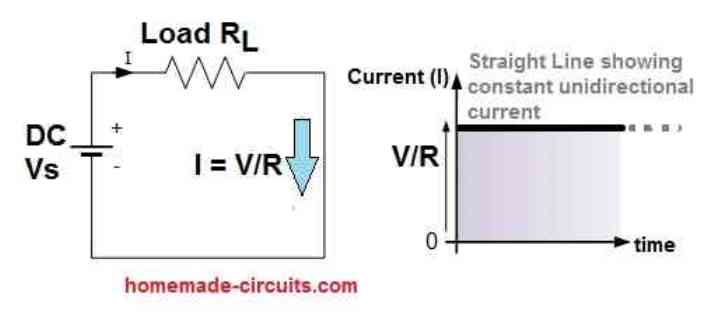
On the other hand, an AC waveform, also known as an alternating function, varies in both magnitude and direction in a more or less even manner over time, making it a "bi-directional" waveform.
An AC waveform can represent either a power source or a signal source, and its shape generally follows that of a mathematical sinusoid, which can be expressed as A(t) = Amax*sin(2πƒt).
The term AC, or Alternating Current, generally refers to a time-varying waveform, with the most common type being a sinusoidal waveform, which is also known as a sine wave.
Sine waves are one of the most important types of AC waveform used in electrical engineering.
An AC waveform can be represented by plotting the instantaneous ordinate values of either voltage or current against time.
It constantly changes its polarity every half cycle, alternating between a positive maximum value and a negative maximum value with respect to time. A common example of an AC waveform is the domestic mains voltage supply used in our homes.
This indicates that the AC waveform is a "time-dependent signal," and the most common type of time-dependent signal is the periodic waveform, which is the product of a rotating electrical generator.
Generally, the shape of any periodic waveform can be generated by using a fundamental frequency and superimposing it with harmonic signals of varying frequencies and amplitudes, but that is beyond the scope of this tutorial.
Unlike direct current (DC), which can be stored in batteries or cells, alternating voltages and currents cannot be stored in the same way.
It is much easier and cheaper to generate these quantities using alternators or waveform generators when they are needed.
The type and shape of an AC waveform depend on the generator or device producing them, but all AC waveforms have a zero voltage line that divides the waveform into two symmetrical halves. The main characteristics of an AC waveform are defined as:
During our lesson on Waveforms, we examined various waveform varieties and defined them as a graphical depiction of how a voltage or current changes over time.
Typically, the baseline of an AC waveform signifies a zero state for either voltage or current. If any section of an AC waveform appears above the zero axis, it denotes a flow of voltage or current in a single direction.
Similarly, a voltage or current flowing in the opposite direction to the first is indicated by any part of the waveform located below the horizontal zero axis.
While sinusoidal AC waveforms typically have an identical shape above and below the zero axis, this is not always true for most non-power AC signals like audio waveforms.
The sinusoidal waveform is the most frequently used periodic signal in Electrical and Electronic Engineering.
However, an AC waveform that oscillates alternately may not necessarily follow a smooth curve defined by the trigonometric sine or cosine function. Alternating current waveforms may also take the shape of complex waves, square waves, or triangular waves, which are illustrated below.
Four Types of Periodic Waveform
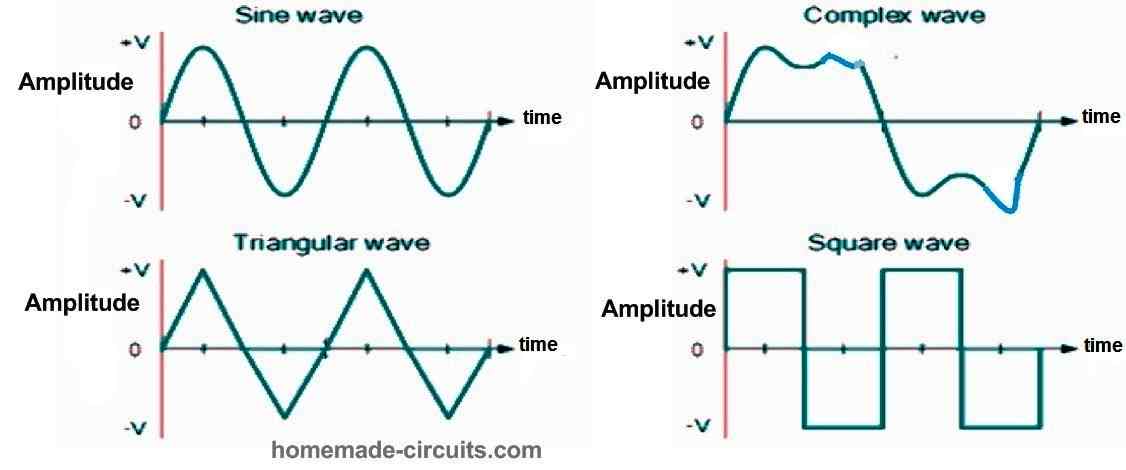
The duration required for an AC Waveform to finish a complete pattern from its positive peak to its negative peak and then return to its zero baseline is referred to as a Cycle. A cycle consists of both a positive half-cycle and a negative half-cycle.
The time it takes for the waveform to complete one full cycle is referred to as the Periodic Time and is represented by the symbol "T."
The number of full cycles produced in a single second (cycles/second) is known as the Frequency, and it is represented by the symbol ƒ. The unit of frequency is the Hertz (Hz), which is named after the German physicist Heinrich Hertz.
It follows that there is a connection between oscillations (cycles), periodic time, and frequency (cycles per second). If a waveform produces ƒ cycles per second, each cycle must take 1/ƒ seconds to complete.
Relationship Between Frequency and Periodic Time
f = 1 / Periodic time = 1 / T Hertz
T = 1 / frequency = 1 / f seconds
Where f denotes Frequency and T denotes Periodic time
First Example of an AC Waveform
We have two questions related to an AC waveform:
- If the frequency of an AC waveform is 50Hz, what would be its periodic time?
- If an AC waveform has a periodic time of 10 milliseconds (ms), what is its frequency?
- T = 1 / f = 1 / 50 = 0.02 seconds or 20 ms
- f = 1 / T = 1 / 10 x 10-3 = 100 Hz
Frequency is a measure of the number of cycles or oscillations of an AC waveform that occur in one second.
The unit used to be expressed as "cycles per second" (cps), but nowadays it is commonly measured in Hertz (Hz).
In residential power systems, the frequency is either 50Hz or 60Hz, depending on the country, and is determined by the rotational speed of the generator.
Since one Hertz is a very small unit, prefixes such as kHz, MHz, and even GHz are used to indicate the order of magnitude of the waveform at higher frequencies.
Frequency Prefixes and their Definitions
| Prefix | Definition | Written as | Periodic Time |
| Kilo | Thousand | kHz | 1ms |
| Mega | Million | MHz | 1us |
| Giga | Billion | GHz | 1ns |
| Terra | Trillion | THz | 1ps |
AC Waveform and its Amplitude
In addition to knowledge of the periodic time or frequency of an alternating quantity, understanding the amplitude, also referred to as the maximum or peak value, is another essential parameter of an AC waveform, which can be represented by terms such as Vmax for voltage or Imax for current.
The peak value refers to the highest point that the waveform reaches during each half cycle, measured from the zero baseline, for either voltage or current. Unlike a DC voltage or current, which has a constant state that can be measured or calculated using Ohm's Law, the value of an alternating quantity is continually changing over time.
For purely sinusoidal waveforms, the peak value is the same for both half cycles (+Vm = -Vm). However, for non-sinusoidal or complex waveforms, the maximum peak value may differ significantly between each half cycle.
Sometimes, an alternating waveform is given a peak-to-peak value, denoted as Vp-p, which is simply the distance or sum in voltage between the maximum peak value, +Vmax, and the minimum peak value, -Vmax, during one complete cycle.
AC Waveform and its Average Value
For a continuous DC voltage, the average or mean value is always equal to its maximum peak value, since the DC voltage remains constant.
The average value will only vary if the duty cycle changes. In contrast, for a pure sine wave, if the average value is computed over the full cycle, it would be zero because the positive and negative halves cancel each other out.
Therefore, to determine the average or mean value of an AC waveform, it is calculated or measured over a half cycle only, as illustrated below.
Non-sinusoidal Waveform and its Average Value
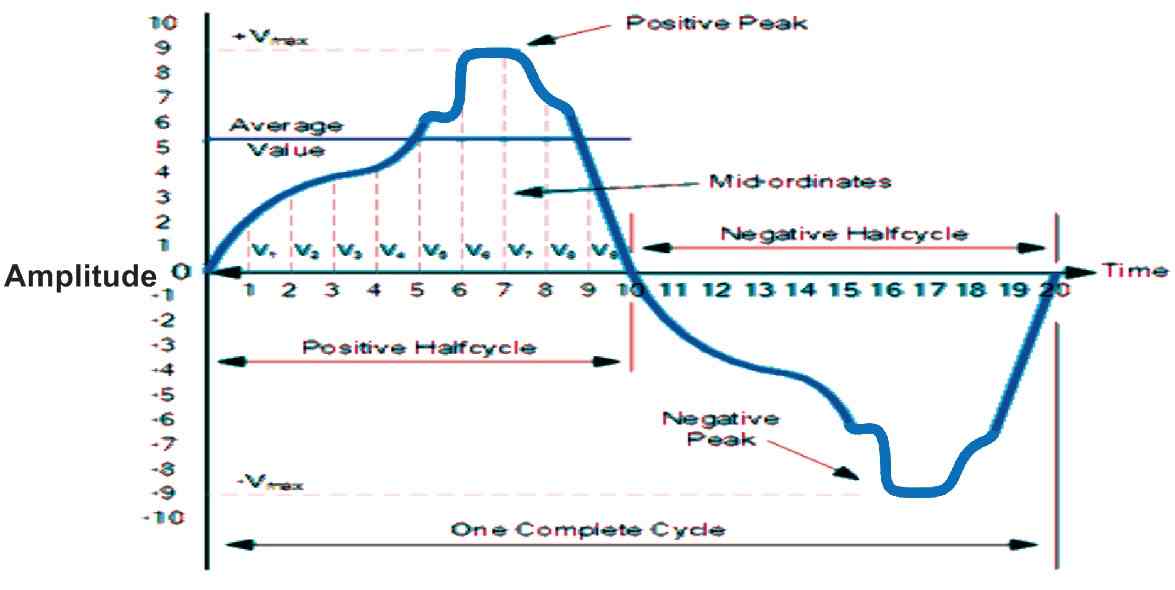
To determine the average value of a waveform, one can use mathematical techniques such as the mid-ordinate rule, trapezoidal rule, or Simpson's rule, which are commonly employed in mathematics to compute the area beneath a curve.
The mid-ordinate rule is an efficient method for approximating the area beneath any irregular waveform.
The zero axis base line is partitioned into a set of equal parts, which in the example given above was nine (from V1 to V9).
The accuracy of the final average or mean value improves as the number of ordinate lines increases. To calculate the average value, all the instantaneous values are summed together and then divided by the total number. The formula for this is:
AC Waveform’s Average Value
V(average) = (V1 + V2 + V3 + V4 + ..... + Vn) / n
In the equation, 'n' represents the precise number of mid-ordinates that were utilized.
For a pure sine wave, the average or mean value is always 0.637 times the maximum peak value (Vmax), and this rule is also applicable for determining the average value of current.
AC Waveform and its RMS Value
The average value of an AC waveform, as determined previously as 0.637 times the maximum peak value, cannot be used as the same value for a DC supply.
This is because an AC waveform is constantly changing over time and has no fixed value, unlike a DC supply, which is constant and of a fixed value.
Therefore, the equivalent value for an AC system that provides the same electrical power to a load as a DC circuit is called the "effective value."
The effective value of a sine wave creates the same I2*R heating effect in a load as a constant DC supply would.
The effective value of a sine wave is commonly referred to as the Root Mean Squared or simply RMS value. It is calculated by taking the square root of the mean (average) of the square of the voltage or current.
The RMS value, denoted by Vrms or Irms, is given by finding the square root of the average of the sum of all the squared mid-ordinate values of the sine wave. The formula for determining the RMS value of any AC waveform is shown below.
Calculating RMS Value of an AC Waveform
VRMS = √[(V1)2 + (V2)2 + (V3)2 + (V4)2 + ...... (Vn)2] / n
Where, n refers to the number of mid-ordinates.
When dealing with a pure sinusoidal waveform, the R.M.S. value is always equal to 1/√2 times the maximum value (Vmax) which is equivalent to 0.707 times Vmax.
This relationship also holds true for the RMS values of current. The RMS value of a sinusoidal waveform is always greater than the average value, except for a rectangular waveform where the heating effect remains constant and the average and RMS values are the same.
It is important to note that most multimeters, whether digital or analogue, only measure the RMS values of voltage and current unless otherwise specified. When measuring a direct current system, the reading will be I = V/R, while for an alternating current system the reading will be Irms = Vrms/R.
When calculating RMS or peak voltages, it is essential to only use VRMS to find IRMS values, or peak voltage (Vp) to find peak current (Ip) values. Mixing them together will result in incorrect Average, RMS, or Peak values of a sine wave.
Understanding Form Factor and Crest Factor
While Form Factor and Crest Factor are not commonly used today, they can provide information about the shape of an AC waveform. Form Factor is the ratio of the average value to the RMS value and is expressed as:
Form Factor = RMS Value / Average Value = 0.707 x Vmax / 0.637 Vmax
The Form Factor, which is the ratio of the average value to the RMS value, is rarely used nowadays. For a pure sinusoidal waveform, the Form Factor is always equal to 1.11. The Crest Factor, on the other hand, is the ratio of the RMS value to the peak value of the waveform and is given as.
Crest Factor = Peak Value / RMS Value = Vmax / 0.707 x Vmax
The Crest Factor of a pure sinusoidal waveform is always equal to 1.414.
Second Example of an AC waveform:
If a sinusoidal AC current of 5 amps is flowing through a 50Ω resistance, we can calculate the average and peak voltages of the supply.
To find the RMS voltage value, we use the following formula:
VRMS = I x R = 5 x 50 = 250 V
For Calculating the average voltage, use this formula:
Form Factor = VRMS / Vaverage = 250 / 1.11 = 2.25 V
For Calculating the peak voltage, use the following formula:
Peak Voltage = RMS x 1.414 = 250 x 1.414 = 353.5 V
The concepts of Average, R.M.S., Form Factor, and Crest Factor are not limited to sinusoidal waveforms. They can also be applied to any periodic waveform, such as triangular, square, sawtooth, or any other complex voltage or current waveform.
However, converting between different types of values for non-sinusoidal waveforms can be challenging. To simplify this process, a conversion table is provided below for easy reference.
| Convert From | Multiply By | Or By | To Get Value |
| Peak | 2 | (√2)2 | Peak-to-Peak |
| Peak-to-Peak | 0.5 | 1/2 | Peak |
| Peak | 0.707 | 1/(√2) | RMS |
| Peak | 0.637 | 2/π | Average |
| Average | 1.570 | π/2 | Peak |
| Average | 1.111 | π/(2√2) | RMS |
| RMS | 1.414 | √2 | Peak |
| RMS | 0.901 | (2√2)/π | Average |
Post your comments here and get guaranteed replies. Comments must be related to the above article.