The Role of Inductor Coil in SMPS

The most crucial element of a switched mode converter or an SMPS is the inductor.

Energy is stored in the form of a magnetic field in the core material of the inductor during the brief ON period (t_on) switched through the connected switching element such as MOSFET or a BJT.

How the Inductor Works in SMPS

During this ON period voltage, V, is applied across the inductor, L, and the current through the inductor changes with time.

This current change is 'restricted' by the inductance, hence we find the related term choke normally used as an alternative name for an SMPS inductor, which is mathematically represented through the formula:

di/dt=V/L

When the switch is turned off, energy stored in the inductor is released or "kicked back".

Magnetic field developed across the windings collapses due to the absence of current flow or voltage to hold the field. The collapsing field at this point sharply 'cuts' through the windings, which builds a reverse voltage having an opposite polarity to that originally applied switching voltage.

This voltage causes a current to move in the same direction. An energy exchange is thus happens between the input and output of the inductor winding.

Implementing the inductor in the above explained manner can be witnessed as a primary application of Lenz's law. On the other hand, at first it seems that no energy could be stored 'infinitely' within an inductor just like a capacitor.

Imagine an inductor built using superconducting wire. Once 'charged' with a switching potential, the stored energy could possibly be held on to forever in the form of a magnetic field.

However, quickly extracting this energy can be a completely different issue. How much energy that could be stashed within an inductor is restricted by the saturation flux density, Bmax, of the core material of the inductor.

This material is usually a ferrite. The moment an inductor runs into a saturation, the core material losses its ability to get magnetized any further.

All the magnetic dipoles inside the material get aligned, thereby no more energy is able to accumulate as a magnetic field inside it. Saturation flux density of the material is generally affected with changes in the core temperature, which may drop by 50% in 100°C than its original value at 25°C

To be precise, if the SMPS inductor core is not prevented from saturating, the current through tends to become uncontrolled due to the inductive effect.

This now solely becomes limited with the resistance of the windings and the amount of current the source supply is able to provide. The situation is generally controlled by the maximum on-time of the switching element which is appropriately limited to prevent saturation of the core.

Calculating Inductor Voltage and Current

To control and optimize the saturation point, current and voltage across the inductor is thus appropriately calculated in all SMPS designs. It is the current change with time that becomes the key factor in an SMPS design. This is given by:

i = (Vin/L)t_on

The above formula considers a zero resistance in series with the inductor. However, practically, the resistance associated with the switching element, inductor, as well as the PCB track will all contribute to limit the maximum current via the inductor.

Let's assume a resistance this to be a total of 1 ohm, which seems quite reasonable.

Thus the Current through the inductor can be now interpreted as:

i = (V_in / R)x (1 - e^-t_onR/L)

Core Saturation Graphs

Referring to the graphs shown below the first graph shows the difference in current through a 10 µH inductor with no series resistance, and when 1 Ohm is inserted in series.

The voltage used is 10 V. In case there isn't any series 'limiting' resistance, can cause the current to surge rapidly and continuously over an infinite time frame.

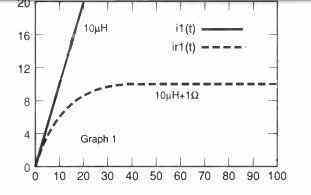
Clearly, this may not be feasible, however the report does emphasize that the current in an inductor could quickly attain substantial and potentially dangerous magnitudes. This formula merely is valid as long as the inductor remains below the saturation point.

As soon as the inductor core reaches saturation, the inductive concentration is unable to optimize the current rise. Therefore the current rises very fast which is simply beyond the prediction range of the equation. During the saturation, the current gets restricted at a value normally established by the series resistance and applied voltage.

In case of smaller inductors the increases in current through them is really fast, but they can retain significant levels of energy within a stipulated timeframe. On the contrary, bigger inductor values may show sluggish current rise through, but these are unable to retain high levels of energy within the same stipulated time.

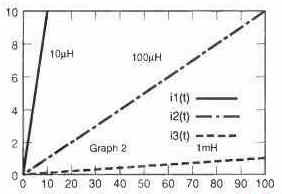
This effect can be witnessed in the second and third graphs, the former demonstrating rise in current in 10 µH, 100 µH, and 1 mH inductors when a 10V supply is utilized.

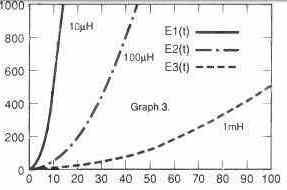
Graph 3 indicates the energy stored over time for inductors with the same values.

In the fourth graph we can see the current rise through the same inductors, by applying a 10 V although now a series resistance of 1 Ohm isinserted in series with the inductor.

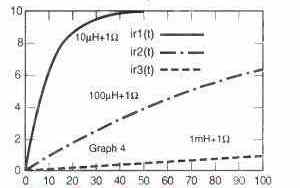
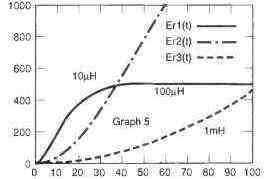
The fifth graph demonstrates the energy stored for the very same inductors.

Here, it is apparent that this current through the 10 µH inductor soars rapidly towards the 10 A maximum value in roughly 50 ms. However as a result of 1 ohm resistor it is able to retain only close to 500 millijoules.

Having said that, current through 100 µH and 1 mH inductors rises and the stored energy tend to be reasonably unaffected with the series resistance across the same amount of time.