In the previous article we learned about ripple factor in power supply circuits, here we continue and evaluate the formula for calculating ripple current, and consequently the filter capacitor value for eliminating the ripple content in the DC output.
The previous post explained how a DC content after rectification may carry the maximum possible amount of ripple voltage, and how it may be reduced significantly by using a smoothing capacitor.
Although the final ripple content which is the difference between the peak value and the minimum value of the smoothed DC, never seem to eliminate completely, and directly relies on the load current.
In other words if the load is relatively higher, the capacitor begins losing its ability to compensate or correct the ripple factor.
Standard Formula for Calculating Filter Capacitor
In the following section we will try to evaluate the formula for calculating filter capacitor in power supply circuits for ensuring minimum ripple at the output (depending on the connected load current spec).
C = I / (2 x f x Vpp)
where I = load current
f = input frequency of AC
Vpp = the minimum ripple (the peak to peak voltage after smoothing) that may be allowable or OK for the user, because practically it's never feasible to make this zero, as that would demand an unworkable, non-viable monstrous capacitor value, probably not feasible for anybody to implement.
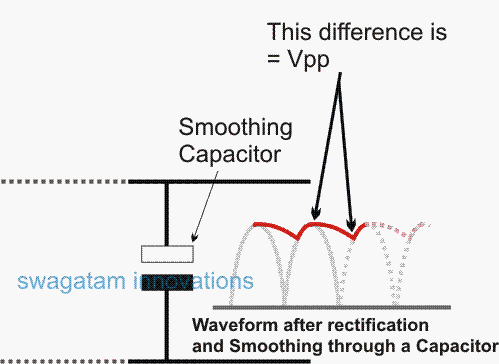
Let's try to understand the relation between load current, ripple and the optimal capacitor value from the following evaluation.
Relation Between Load Current, Ripple, and Capacitor Value
In the mentioned formula we can see that the ripple and the capacitance are inversely proportional, meaning if the ripple needs to be minimum, the capacitor value needs to increase and vice versa.
Suppose we agree to a Vpp value that's, say 1V, to be present in the final DC content after smoothing, then the capacitor value may be calculated as shown below:
Example:
C = I / 2 x f x Vpp (assuming f = 100Hz and load current requirement as 2amp))
Vpp should be ideally always a one because expecting lower values can demand huge unpracticable capacitors values, so "1" Vpp can be taken as a reasonable value.
Solving the above Formula we get:
C = I / (2 x f x Vpp)
= 2 / (2 x 100 x 1) = 2 / 200
= 0.01 Farads or 10,000uF (1Farad = 1000000 uF)
Thus, the above formula clearly shows how the required filter capacitor may be calculated with respect to the load current and the minimum allowable ripple current in the DC component.
By referring to the above solved example, one may try varying the load current, and/or the allowable ripple current and easily evaluate the filter capacitor value accordingly for ensuring an optimal or the intended smoothing of the rectified DC in a given power supply circuit.
I am trying to build a 250 to 300 volt 5 to 6 amp power supply or battery charger to charge the battery on my 03 Prius thanks if you can help
You can build the auto cut off circuit by referring to the following circuit:
https://www.homemade-circuits.com/high-voltage-360v-battery-charger/
I do not understand. So you should have a capacitor of 20000uf in the example above?
C = I / 2 x f x Vpp
= 2 / 2 x 100 x 1
= 0.01 Farads or 10,000uF (1Farad = 1000000 uF)
Where did you get the decimal point from?
I’m trying to figure out the size of capacitor for a kbpc3508 diode bridge rectifier.
C = I / (2 x f x Vpp)
= 2 / (2 x 100 x 1)
= 2 / 200
= 0.01 Farads
0.01 Farads is 10000uF and not 10,000uF or i am wrong here?
sir, your circuit is great but i have questions to you …how did you do ?
very good post and site
and about calculating filter capacitor voltage what’s your idea?
Thank you Jack!
Thank you so much for your clarification. You have helped so much.
You are welcome!!
A very good post that I have learnt a lot. Please how do we measure/calculate/obtain the Vpp?
I am glad you liked!!
Vpp is the final ripple that may appear with the DC after rectification, and it is supposed to be zero ideally, but in the practical world a zero ripple cannot be possible, and moreover that would demand a huge filter capacitor…therefore we assume this value to be around “1” for all filter capacitor calculations
Sir output of my transformer after rectification is 11.9v I want to charge my 12v battery please suggett the capacitor rating I want to use here to charge my battery please reply fast
Vijay, if you are interested t calculate the exact value of the capacitor then you'll need to evaluate charging current first, which can be found by dividing the AH of your battery with 10.
In general you can simply use the highest value capacitor that may be feasible for you.
Dear Sir,
For SMPS (step down) out put capacitor calculation whether we have to take switching frequency as "f" in the formula? please clarify
Dear Raveesh, in SMPS, the waveform is rectangle or square and also the duty cycle factor is present…so may be the "F" could be differently expressed here in terms of duty cycle %….not much sure about it right now…
Sir, I have seen more number of inverter circuits on your site. Can u suggest the circuit which should produce an exact sinewave as same grid supply.
Vijay, trying to acquire an analogue sinewave replication can make an inverter inefficient, that's why all inverers rely on PWM which is much suited with digital inverters and are able to deliver max efficiency… and also a waveform quite similar to a pure sine wave.
Sir I planned to design an inverter for my home which should light up 3,20 watt cfl bulb and also for mobile charging.hence I assumed that my total watt requirement is not more than 100watt.please suggest any circuit based on my requirement and say the information about the battery that I need to use for operating an inverter for 5 hours.
Vijay, you can try the following circuit:
https://www.homemade-circuits.com/2012/09/mini-50-watt-mosfet-inverter-circuit.html
the battery should be rated at at least 12V, 75 AH
the inverter is capable of handling up to 200 watts if the trafo is appropriately rated
Nice post sir really useful information.
thanks Vijay, I am glad you liked it….
nice post sir.really helpful….. thanks sir
It's my pleasure Alamgir