Whenever brakes are applied in any vehicle, a lot of energy is wasted in the process of stopping the vehicle mass and again restoring the mass back to its original speed. The simple idea designed by me appears to be quite effective in solving this issue. I will explain more about this simple regenerative braking concept.
How Energy is Wasted in Vehicles
A vehicle is a heavy mass which requires relatively significant amount of energy to initiate its movement from a stationery condition until the desired speed is achieved, after this the energy required for sustaining the vehicle speed becomes easier and nominal. This is because the potential energy stored inside the vehicle now gets converted into kinetic energy and assists the engine in sustaining the speed with comparatively less effort.
However when the vehicle is required to be stopped or when brakes are applied, this kinetic energy developed during the motion is resisted which results in a wasted energy. On top of this when the vehicle is started again, it yet again consumes the same amount of energy to get back to its earlier speed...that's a double wasted energy encountered in the vehicle while braking and starting, and this might happen many times during a course of journey.
This wastage of precious fuel may result in a cut down in the efficiency by over 40% especially if the journey is riddled with traffics and uneven roads or zig zag roads.
How Regenerative Braking Helps
A simple idea as developed by me (assumably), can take care of the above situation very effectively, and can restore the efficiency by at least 30%.
We all at some point of time in our life have used a bicycle, and we all pretty well know how its rear wheel mechanism is designed and configured with the pedals.
That's right, the rear wheels are geared with the pedal mechanism in such a way that while the pedals are moved the rear wheel responds to it and moves the rider and the bike forward, but interestingly the movement is sustained even during instances when the rider stops pedalling and the pedal gear is not moving.
The rear wheel makes sure that once initiated it keeps moving regardless of the pedal gear movement, by using the stored kinetic energy in the load (rider), during situations when the vehicle is idle and the pedal is not in an energized mode.
Implementing Bicycle Rear Wheel Mechanism
The same concept or mechanism (ratcheting freewheel mechanism) can be simply implemented in all motor vehicles for retrieving the kinetic energy back in favor of the vehicle whenever brakes are applied.
The dimensions of the wheel and the gear mechanism needs to be appropriately modified for a particular vehicle as per its mass.
The idea of the proposed regenerative braking mechanism can be witnessed below:
Designing a Regenerative Mechanism System
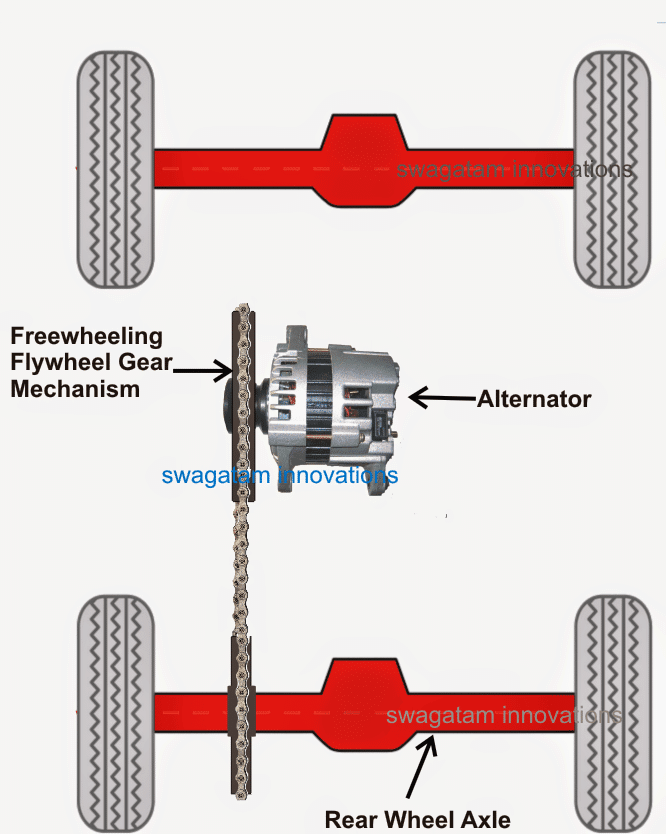
The rear wheel of the bicycle can be seen replaced with a proportionately heavier flywheel, and this flywheel is geared up through a locking chain with another gear fixed with the axle of the vehicle wheel.
The flywheel is attached with an alternator for converting its rotations into electricity.
How much Can Regenerative Concept Save Energy
The above regenerative braking concept can be expected to retrieve up to around 70% of the braking wasted energy into electricity which is stored in the battery and later on facilitate quicker ignition starting of the vehicle.
If an electricity conversion is not felt necessary, the alternator may be simply eliminated and the flywheel may be left alone for freewheeling during a braking action, this freewheeling flywheel would then assist the vehicle to regain its lost speed once the brakes are removed and a pick-up is initialized, making sure that a significant amount of wasted braking energy is returned to the vehicle and the overall efficiency is improved.

Great job
THANKS
Swagatam
Very good idea. It can be worked on.
However, the automotive alternator needs quite a lot of torque to rotate the armature when the field winding is powered on. I am afraid that a regular automotive alternator might not perform well with the above idea. A permanent magnet type alternator will definitely give better results.
For a permanent magnet type alternator, the charging system will be shunt-type similar to that of motorcycles. And that also involves energy wastage.
Overall, your idea is good. Might need some modification to make it work.
Thanks Abu-Hafss,
a car alternator is perhaps the one of the most efficient generators, and if it requires more torque then it must be producing that much more electricity, right? and moreover here we are applying the flywheel concept, which is attributed for handling a heavier load….
but anyhow the user is free to use any type of generator as they wish, for the conversions, or can simply eliminate it and prefer to recycle the kinetic energy of the flywheel…..