In this post we are going to understand how LC oscillator circuits functions and we will be constructing one of the popular LC based oscillator - Colpitts oscillator.
What are Oscillators
Electronic oscillators are used in most of our daily used electronic gadgets ranging from digital clock to high end core i7 processor. Oscillators are heart of all digital circuits but, not only digital circuit employee oscillators but also analogue circuits uses oscillatory circuits.
For instant AM, FM radio, where the high frequency oscillation is used as carrier signal to transport message signal.
There are many different kinds of oscillators such as RC, LC, crystal etc. Each one of them has their own advantages and disadvantages. So there is nothing called best or ideal oscillator, we have to analyse the circumstance of our circuit and choose the best one which suit, that’s why we find wide range of oscillators in every day used gadgets.
LC Oscillators
Let’s dive into the explanation of LC oscillator.
The LC oscillator consists of an inductor and a capacitor as shown in figure below.
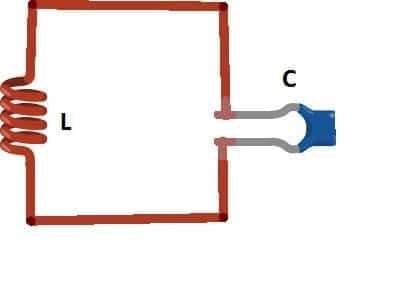
The value of the capacitor and resistor determines the output oscillation. So how do they generate oscillation?
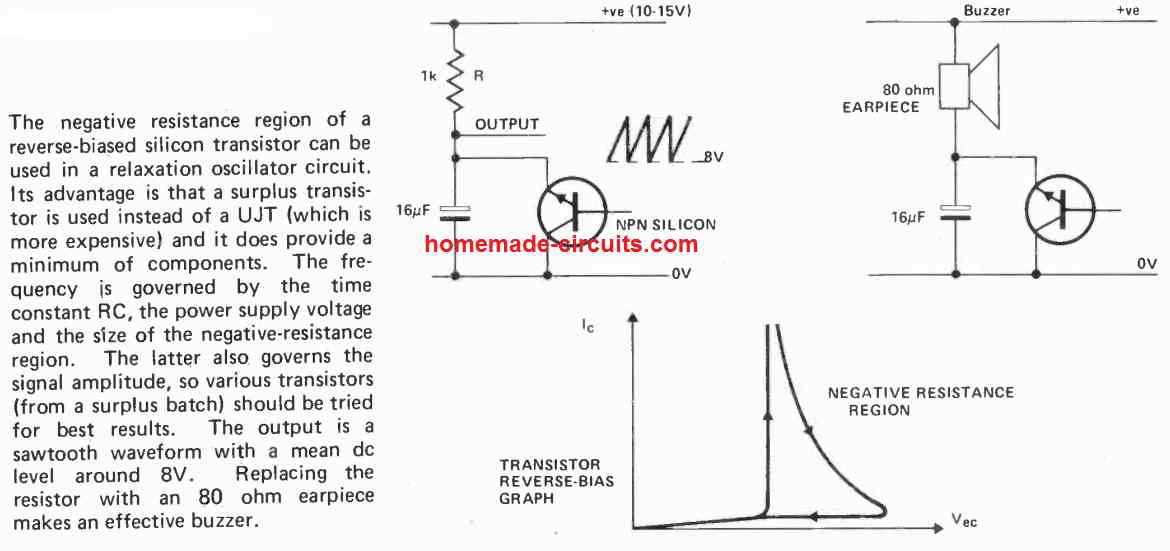
Well, we need to apply external energy between L and C i.e. voltage. When we apply the voltage, the capacitor gets charged-up. When the supply is cut-off, the stored energy from capacitor flows to inductor and inductor starts building magnetic field around it until the capacitor completely gets discharged.
When the capacitor is fully discharged, the magnetic field around inductor collapse and induces voltage and charge-up the capacitor with opposite polarity and the cycle repeats.
The charge and discharge between L and C produces oscillation and this oscillation is called resonance frequency. However the frequency generation won’t last forever due to parasitic resistance which dissipates the energy in the oscillatory circuit in the form of heat.
To maintain the oscillation and use the oscillation with reasonable output strength, we need an amplifier with zero degree phase shift and feedback.
The feedback feed small amount of output from amplifier back to LC network to compensate the loss due to parasitic resistance and maintain the oscillation. Thus we can generate steady sine wave output.
Application circuit:
Here is a colpitts oscillator circuit which can generate around 30 Mhz signal.
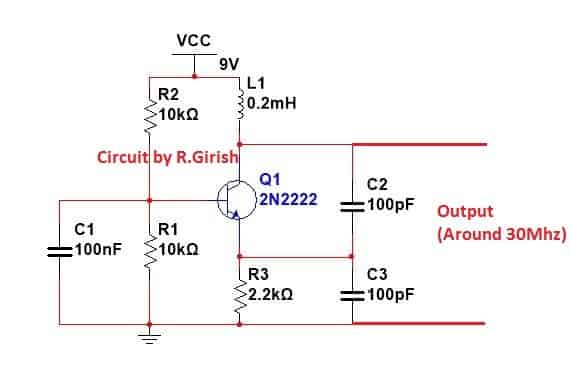
A couple of factors are essential to maintain oscillations in transistorized LC resonant crystal oscillator circuits. First, the feedback voltage arriving from the transistor collector has to be in phase with the actual input excitation voltage which is initially applied on the base of the transistor.
In other words the feedback link of the circuit should be positive or regenerative in nature.
Second, the quantity of the feedback energy to the base network should be adequately strong to compensate for the energy losses encountered in the base circuit. It can be necessary to evaluate the theory of Q prior to talking about oscillator functioning.
Q is described as a magnitude of caliber in a resonant circuit. Equivalent to the reactance divided by the resistance, the Q factor symbolizes the capability of the circuit to maintain oscillations using bare minimum feedback.
To put it briefly, the larger the Q the greater the efficiency of the resonance stage of the circuit. The inherent Q of quartz can be 10 million at 1 MHz frequency.
Even though Q mgnitude for a attached resonator crystal is diminished to ranges of 20,000 to more than a million, it is still well over the figures that's much superior to the top LC resonator or LC tank circuit.
LC oscillator with Crystal
The extremely large Q of the crystal oscillator substantially minimizes frequency drift triggered by temperature and the DC voltage fluctuations.
Furthermore, crystal-controlled oscillators generate a reduced amount of noise compared to traditional LC tank based oscillator circuits, and hence produce a healthier output signal. The easiest crystal oscillator is made up of solitary BJT using a basic feedback network.
Figure 1-a displays a block diagram of a universal crystal oscillator. In this concept , an NPN BJT based amplifier can be seen configured with three feedback circuits. Suitable DC bias is presumed to be present although not revealed in the diagram.
Figure 1-b is an comparative circuit built using the parts L1 and C1, and C2 as shown. Each and every crystal oscillator circuit discussed below are designed to work with exactly the same fundamental topology, by using a minimum of two capacitors and an inductor. The crystal could be seen as an element of the feedback circuit.
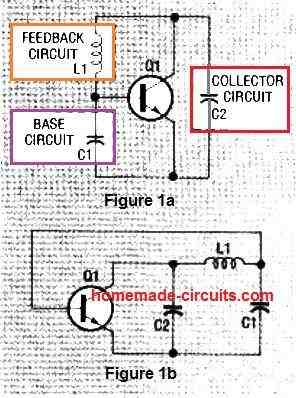
Capacitors C1 and C2 consist of residual transistor and junction capacitance. Capacitor C2 is similar to a parallel network of an inductor and a capacitor.
This LC pair works like the crystal's third overtone selector since it exihibits capacitive nature only at the crystal's overtone frequency, and inductive property at its fundamental frequency.
Therefore, an inductor positioned at C2 inhibits oscillation at the crystal's fundamental frequency. Along with amplification and feedback, an oscillator circuit additionally needs a limiting factor, that occurs when a rise in the input signal no more results in a rise in the output signal. Because of this, the oscillator's output attains a boundary and continues to be in this boundary.
The typical Colpitts crystal-controlled oscillator possesses a stringent load and tuning specifications, while the a pair of semi-isolated models are much less demanding, and are proposed as far better options for general-purpose applications.
In case you are looking for a very accurate output frequency, the Pierce crystal oscillator is the one you must opt for.
On the other hand, if you just want to try things out with oscillators, you may realize that the Butler circuit is able to oscillate without depending on a crystal, and you could test the results using a crystal in or out.
General Colpitts oscillators
A couple of variations of the Colpitts crystal-controlled oscillator are introduced in this article: the standard and the semi-isolated.
The standard circuit, demonstrated in Fig. 2, is dependent on the specifications of both, the crystal and load resistance. Additionally, its output power is restricted to less than 50 % of the crystal's power dissipation. However, it is yet considered to be one of the favorites.
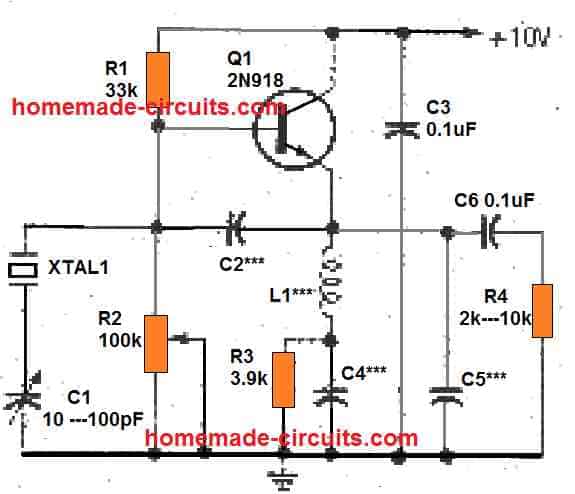
Resistors R1, R2, and R3 provide the DC bias to the transistor Q1. Potentiometer R2 is used to enable up to around 1.5 milliamperes of emitter current. Capacitors C3, C4, and C6 work like a bypass elements for the radio frequency at XTAL1's working frequency (fundamental or overtone).
Capacitor C2 operates like the feedback base circuit, equivalent to the capacitor C1 as explained in in Fig.1. When the circuit is working at the XTAL1's operating frequency, L1 and C5 exhibit a net capacitive reactance, and therefore function as the collector circuit feedback capacitor, just like C2 in Figure1.
When overtone crystals are utilized, L1 and C5 behave just like an overtone selector, blocking oscillation at the crystal's fundamental frequency. Capacitor C1 which is an adjustable trimmer, tweaks the feedback component L1. As the C1 value is reduced, the oscillator's output frequency increases.
Another Crystal Controlled Colpitts Oscillator
Next up is a tapped capacitor setup, also known as a Colpitts oscillator circuit, which is controlled by a crystal. The feed-back ratio required to sustain oscillation is determined by the values of C1 and C2.
The values of C1 and C2 should be chosen for a particular frequency in order to achieve the best level of output and frequency stability. Here, some experimentation will be necessary. Experimental research is enjoyable and a useful approach to learn.
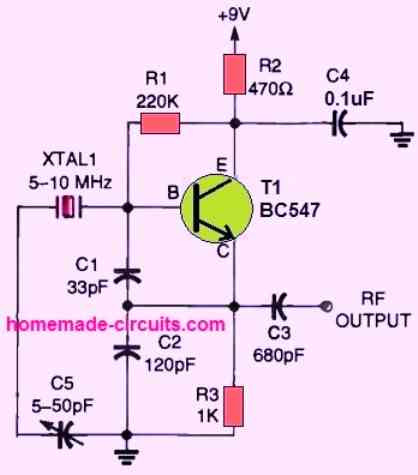
Simple RC Oscillator Circuit
An oscillator can be also built using just a resistor, capacitor network along with a transistor. Here the transistor base terminal is kept unconnected, only the emitter and collector are used.
The complete circuit diagram for this RC oscillator can be seen in the following image:
Simple LC RF Oscillator
The Colpitts circuit presented in the following figure is a simple LC RF oscillator that can work nicely between around 100kHz to 50MHz or higher. Transistor TR1 is configured like a source follower, and the tiny coupling via the T1 inductor winding on is implemented to generate a positive feedback and for stepping up the voltage required for sustaining the oscillation.
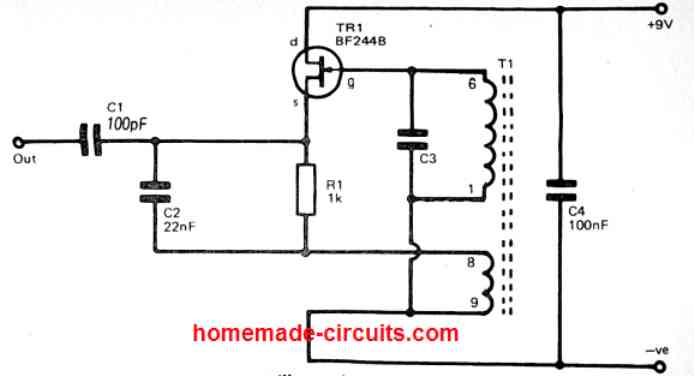
The primary winding of T1 along with C3 form the LC tuned circuit. This establishes the operating frequency of the LC oscillator circuit. R1 works like the source load for TR1 at the supplied DC, however TR1 gets bypassed with an AC through C2 causing the coupling winding of T1 to form the real source load for Tr1.
The output signal of the oscillator is derived through the TR1 source via the DC blocking capacitor C1. Capacitor C4 is simply works like a supply decoupling capacitor. In case an adjustable tuning oscillator is expected, C3 could be easily be replaced with a variable capacitor, or a collaboration of fixed and variable capacitors to enable the required tuning range.
For medium and high frequency LC oscillator, many hobbyists employ ready-made coils nowadays, and these usually offer improved and much more predictable frequency outputs, than the basic home-wound coils.
To build T1 at home, just wind two sets of coils (6 to 1, and 8 to 9) one above the other over a small ferrite rod. The number of turns can be experimented for getting different frequency outputs.
The key thing to remember is that the phasing of the smaller coupling winding has to be properly connected, otherwise the circuit will not oscillate. However, the best technique of connecting the smaller coil can be implemented by only through some trial and error.
Have Questions? Please Comment below to Solve your Queries! Comments must be Related to the above Topic!!