The circuit discussed below is designed to generate precision sine and cosine waveforms, which are perfectly identical with their dimensions, but are 90° out of phase.
There are a variety of applications which often demand a couple of sinewave frequencies which are of the identical frequency, but 90° out of phase.
Simply put, a sine signal and a cosine signal together from a single package.
This kind of signals are widely-used in SSB and quadrature modulation, electronic systems of circles and ellipses and conversions involving rectilinear and polar coordinates.
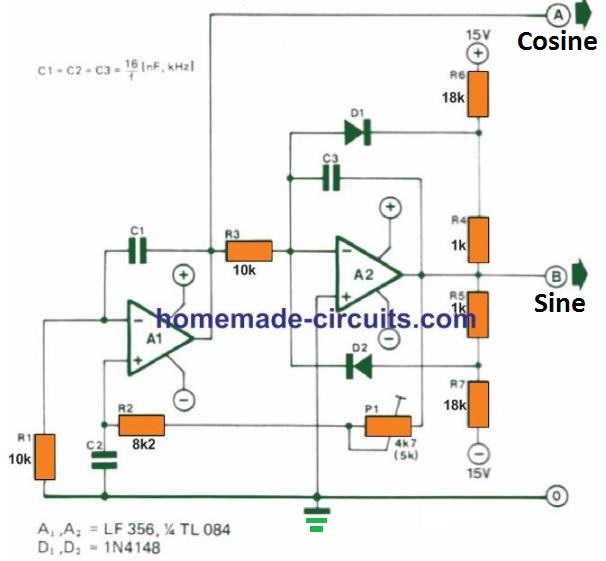
Sine and cosine signals could be acquired from a quadrature oscillator that includes a couple of integrators configured as demonstrated in the diagram.
In the shown diagram, A1 is wired like a non-inverting integrator, while A2 is rigged in the form of an inverting integrator.
How the Circuit Works
The reason why this circuit would generate a sine and cosine signal might not be quickly evident, nevertheless can be easily described.
At output B shows up a signal that is a function of time, f(t). Since this is, minus the integral of the signal at A, it is very clear that the signal at A is, minus the differential of the signal at B, that is - df / dt.
In the same manner, the input signal at the integrator A, that is - d2 f / dt2
However, we also find that the signal at the input of A1 is also the output signal of A2.
Therefore, - d2 f / dt2 = f(t)
These conditions are fulfilled through the sine-cosine signals, because if
f(t) = sin ω t (output B)
d(sin ω t) /dt = cos ω t (output A)
d(cos ω t) /dt = d2(sin ω t) / dt2 = -sin ω t = -f(t)
Output A as a result generates a cosine signal and output B a sine signal. P1 can be used to alter the loop gain of the circuit to ensure that it oscillates without any issues or errors.
In case, may be on account of part tolerances, the circuit fails to oscillate at a set adjustment of P1, you may need to to increase its value to 10 k.
D1, D2 and R4 to R7 are used to stabilize the amplitude of the signal. The sine-cosine frequency rate could be modified by replacing other desired values of capacitor for C1 to C3, by evaluating them through the explained formulas.
