In this post I have explained how to design audio filter circuits such as high pass filter and low pass filter circuits effortlessly without going through the hassles of complex simulation and calculations. The presented designs will enable creating filter circuits only for the desired specific frequency bands and block all other unwanted frequencies.
What's High Pass Filter
As the name suggests a high-pass filter circuit is designed to attenuate all frequencies below a particular selected frequency, and pass or allow all frequencies above this threshold. The principle is just opposite to a low-pass filter circuit.
The cut-off range is generally at a relatively higher frequency range (in kHz),
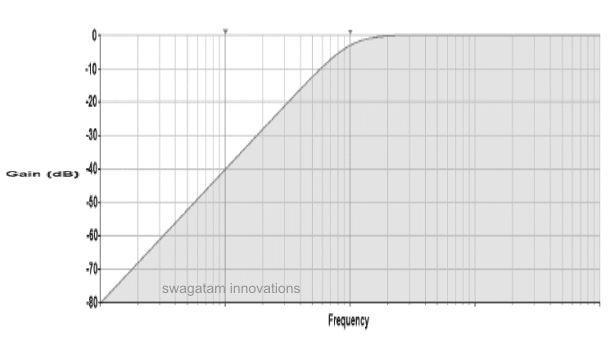
The following high pass filter response graph shows the waveform image indicating how all frequencies below a selected cut-off threshold are attenuated or blocked gradually, as frequency decreases.
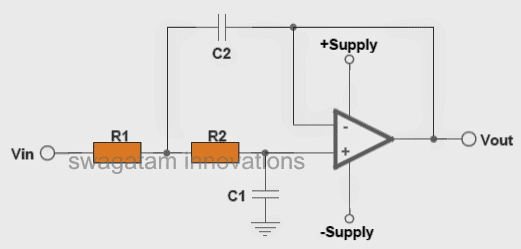
The following two images are configured as standard high-pass filter circuits, where the first one is designed to work with a dual supply whereas the second one is specified to operate with a single supply.
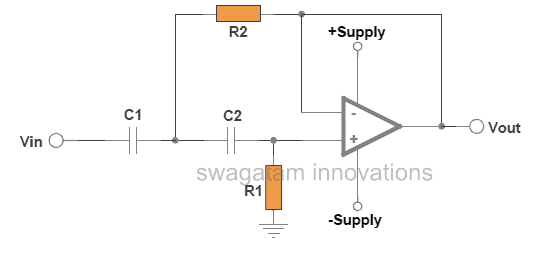
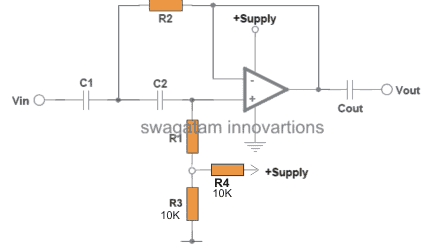
In both the above configurations, the opamp forms the central processing active component, while the associated resistors and capacitors wired across the input pins of the opamp are introduced for determining the high-pass filter cut-off point, depending upon how the values of these passive components are calculated as per the users specifications or requirements.
How to Design a Customized High Pass Filter
As proposed, to design a high-pass filter circuit quickly, the following formulas and the subsequent steps can be used for calculating the relevant resistors and capacitors.
First, select an appropriate value arbitrarily for C1 or C2, both can be identical.
Next, calculate R1 by using the following formula:
R1 = 1 / √2 x π x C1 x Frequency
Here the term "frequency" refers to the desired high-pass cut-off threshold below which other unwanted frequencies need to be attenuated or ignored gradually.
Finally, calculate R2 in the same way as above using the following equation:
R2 = 1 / 2 √2 x π x C1 x Frequency
The single supply version of the high pass filter circuit can be seen involving another capacitor Cout which is not at all critical and can be approximately 100 or 1000 times more than C1.
The above discussions shows how simply anybody can calculate and design a high-pass filter circuit quickly for a particular application which could be a treble control circuit, a 10 band graphic equalizer or a home theater circuit etc.
How Low Pass Filters Work
As the name suggest low pass filter circuits are designed to pass or conduct a preferred range of frequency lower or below a desired cut-off threshold, and attenuate or gradually block the frequencies above this value.
Normally opamps are employed for making such filter circuits, since opamps are best suited for these applications due to their extremely versatile characteristics.
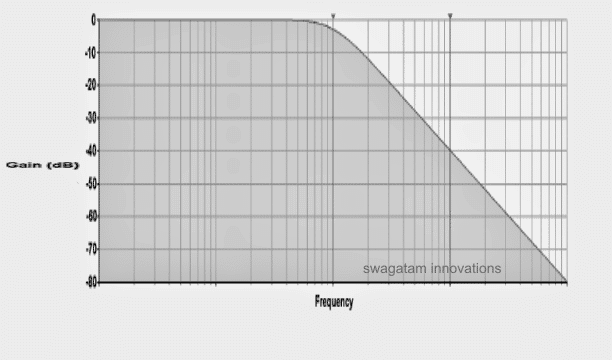
Graph Showing Frequency vs Gain
The following graph provides the typical low pass filter frequency response with regards to the gain, we can clearly see how the response attenuates (gradually drops) as the frequency increases past the particular cut-off threshold.
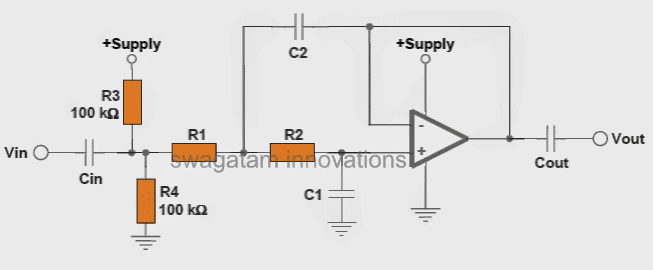
The following images depict the standard opamp based low pass filter circuits. The first one needs to be powered by a dual supply, and the second one works using a single supply voltage.
Designing a Customized Low Pass Filter Circuit
The components R1, R2, and C1, C2 configured with the non-inverting (+) and the inverting (-) input pinouts of the opamp basically decide the cut-off range of the filter, and these need to be calculated optimally while designing the circuit.
For calculating these parameters and designing a low pass filter circuit quickly within minutes one can utilize the following formulas and the explained steps:
First we need to find C1 which we can do by selecting any value arbitrarily as per our convenience.
Next, we can calculate C2 with the formula:
C2 = C1 x 2
R1 and R2 can be identical, and can be calculated using the following formula:
R1 or R2 = 1 / 2 √2 x π x C1 x Frequency.
here the "frequency" is the range where the cut-off transition is expected to happen, or the desired cut-off range.
The values of Cin and the Cout shown in the single supply low pass filter are not critical and these can be anything 100 to 1000 times that of C1, meaning if you selected C1 as 0.1uF, then these could be anywhere between 10uF and 100uF etc. The voltage spec may be selected to be twice that of the supply voltage used.
The resistors are all 1/4 watt rated, 5% or 1%.
That's it!.... using the above simple technique you can design a reasonably good low pass filter quickly and use it for a specific application which could include a high bass music circuit, an active speaker cross over network or a home theater system etc.
High Pass, Low Pass and band Pass from a Single Circuit
A state variable filter such as the one shown below can generate three outputs: high pass, band-pass, and low pass. This is therefore an extremely flexible filter design, specially if the resonant frequency is featured to be adjustable.
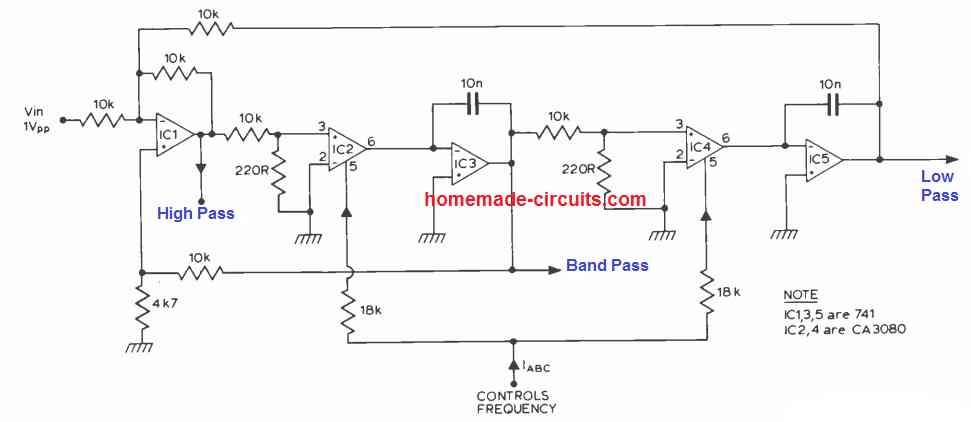
In the proposed filter design, this specific resonant frequency is linearly proportional to the gain of the two integrators. A couple of CA3080's, (IC2, 4) are actually configured to supply the adjustable gain, the resonant frequency being held proportional to the current IABC.
Working with 741 op amps for IC3 it may be possible to get a control range of 100 to 1, (resonant frequency). If the ICs CA3140's are applied in place of 741's then this range could be expanded to practically 10,000 to 1.
More Info: https://drive.google.com/file/d/1yo_WH0NzYg43ro_X0ZrXoLYSM5XOzKU8/view?usp=sharing
