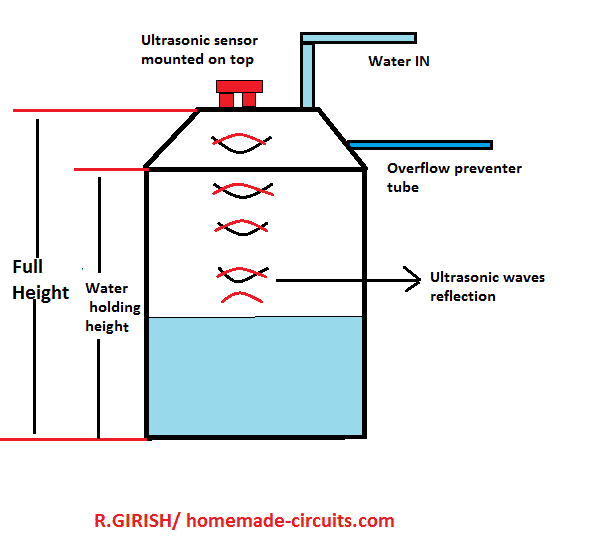
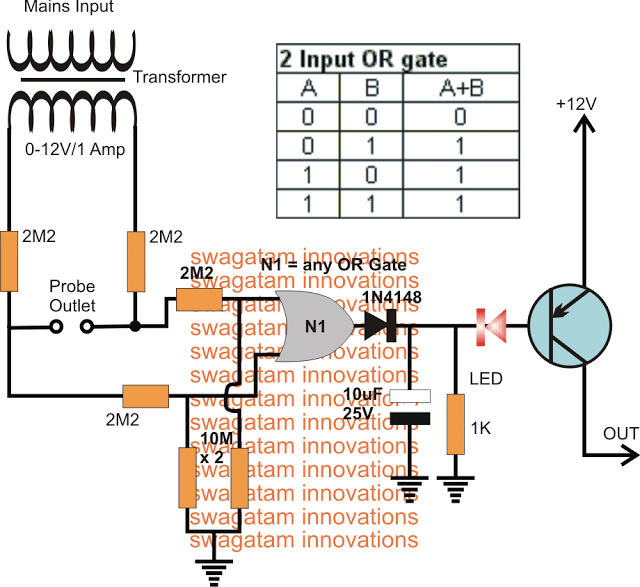
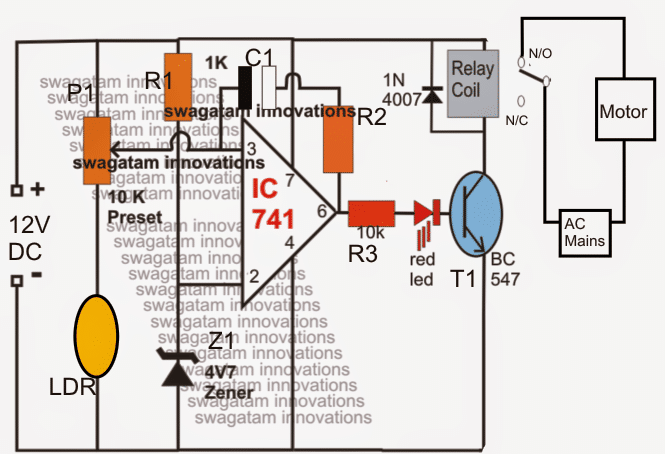
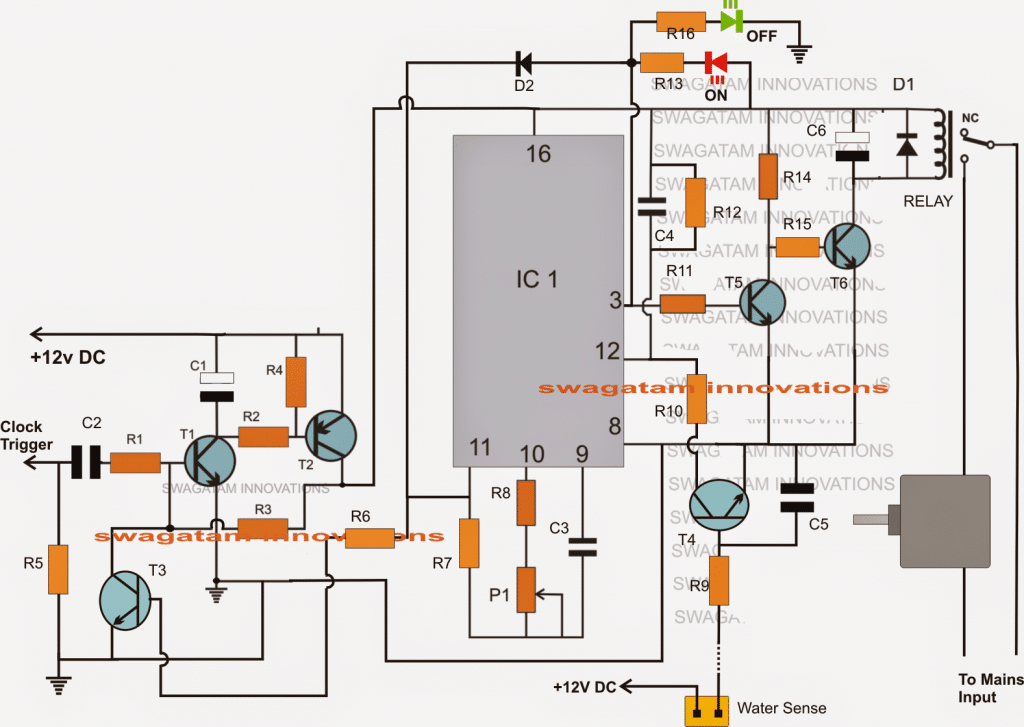
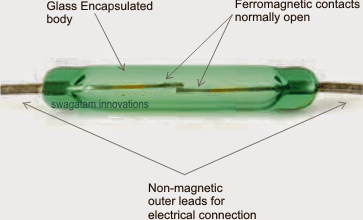
An ultrasonic water level controller is a device which can detect water levels in a tank without a physical contact and send the data to a distant LED indicator in […]
Search Results for: water level
Anti-Corrosion Probes for Water Level Controller
In this post I will explain a few interesting methods of constructing anti-corrosion probes for water level sensor and controller circuits by using alternating supply across the probes. Using Bridge […]
Light Activated Water Level Controller Circuit
The light activated water level controller circuit explained here has the advantage of being corrosion free and much reliable than the traditional moisture sensor type of water sensors. Circuit Operation […]
Digital Clock Activated Water Level Controller Circuit
An automatic clock time triggered water level controller circuit which responds to a real time clock input is discussed in the following article. The design also includes a water detection […]
Making a Float Switch Circuit for a Corrosion-free Water Level Control
A float switch is a device which detects a fluid level (such as water) and activates a set of contacts which may be further integrated to a control circuit for […]
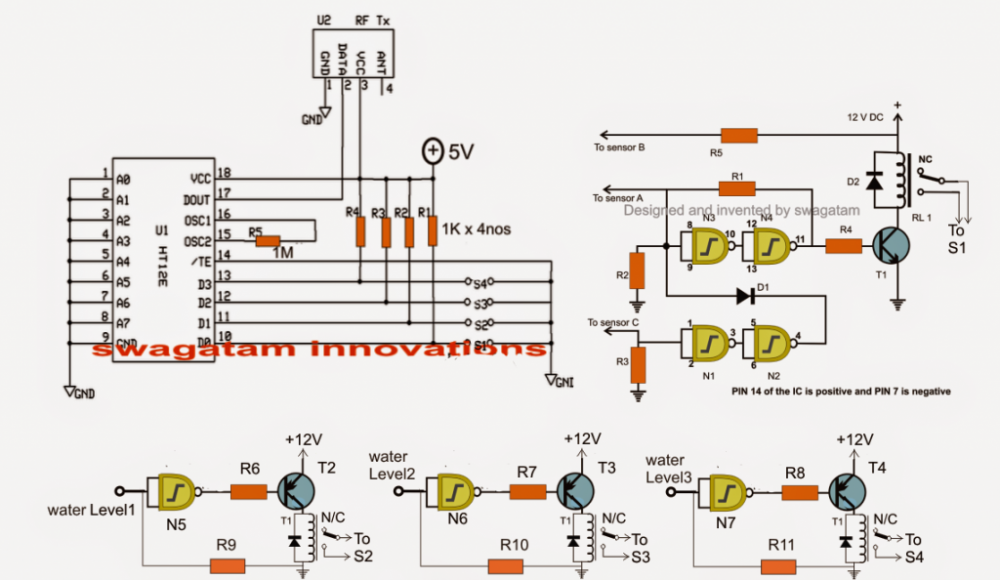
Remote Controlled Wireless Water Level Controller Circuit
For multi-storey buildings where water tanks could be at considerable heights over building terraces, monitoring the levels automatically could become a major issue. RF remote control modules have become pretty […]