Calculating ferrite transformer is a process in which engineers evaluate the various winding specifications, and core dimension of the transformer, using ferrite as the core material. This helps them to create a perfectly optimized transformer for a given application.
The post presents a detailed explanation regarding how to calculate and design customized ferrite core transformers. The content is easy to understand, and can be very handy for engineers engaged in the field of power electronics, and manufacturing SMPS inverters.
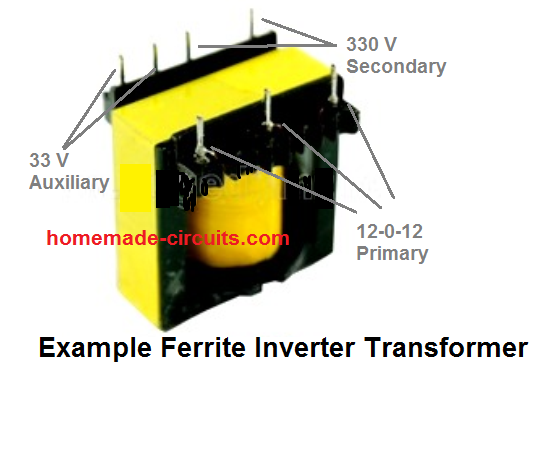
Why Ferrite Core is used in High Frequency Converters
You might have often wondered the reason behind using ferrite cores in all modern switch mode power supplies or SMPS converters. Right, it is to achieve higher efficiency and compactness compared to iron core power supplies, but it would be interesting to know how ferrite cores allow us to achieve this high degree of efficiency and compactness?
It is because in iron core transformers, the iron material has much inferior magnetic permeability than ferrite material. In contrast, ferrite cores possess very high magnetic permeability.
Meaning, when subjected to a magnetic field, ferrite material is able to achieve a very high degree of magnetization, better than all other forms of magnetic material.
A higher magnetic permeability means, lower amount of eddy current and lower switching losses. A magnetic material normally has a tendency to generate eddy current in response to a rising magnetic frequency.
As the frequency is increased, eddy current also increases causing heating of the material and increase in coil impedance, which leads to further switching losses.
Ferrite cores, due to to their high magnetic permeability are able to work more efficiently with higher frequencies, due to lower eddy currents and lower switching losses.
Now you may think, why not use lower frequency as that would conversely help to reduce eddy currents? It appears valid, however, lower frequency would also mean increasing the number of turns for the same transformer.
Since higher frequencies allow proportionately lower number of turns, results in transformer being smaller, lighter and cheaper. This is why SMPS uses a high frequency.
Inverter Topology
In switch mode inverters, normally two types of topology exits: push-pull, and Full bridge. The push pull employs a center tap for the primary winding, while the full bridge consists a single winding for both primary and secondary.
Actually, both the topology are push-pull in nature. In both the forms the winding is applied with a continuously switching reverse-forward alternating current by the MOSFETs, oscillating at the specified high frequency, imitating a push-pull action.
The only fundamental difference between the two is, the primary side of the center tap transformer has 2 times more number of turns than the Full bridge transformer.
How to Calculate Ferrite Core Inverter Transformer
Calculating a ferrite core transformer is actually quite simple, if you have all the specified parameters in hand.
For simplicity, we'll try to solve the formula through an example set up, let's say for a 250 watt transformer.
The power source will be a 12 V battery. The frequency for switching the transformer will be 50 kHz, a typical figure in most SMPS inverters. We'll assume the output to be 310 V, which is normally the peak value of a 220V RMS.
Here,the 310 V will be after rectification through a fast recovery bridge rectifier, and LC filters. We select the core as ETD39.
As we all know, when a 12 V battery is used, it's voltage is never constant. At full charge the value is around 13 V, which keeps dropping as the inverter load consumes power, until finally the battery discharges to its lowest limit, which is typically 10.5 V. So for our calculations we will consider 10.5 V as the supply value for Vin(min) .
Calculating the Primary Turns
The standard formula for calculating the primary number of turns is given below:
N(prim) = Vin(nom) x 108 / 4 x f x Bmax x Ac Here N(prim) refers to the primary turn numbers. Since we have selected a center tap push pull topology in our example, the result obtained will be one-half of the total number of turns required.
- Vin(nom) = Average Input Voltage. Since our average battery voltage is 12V, let's, take Vin(nom) = 12.
- f = 50 kHz, or 50,000 Hz. It is the preferred switching frequency, as selected by us.
- Bmax = Maximum flux density in Gauss. In this example, we'll assume Bmax to be in the range of 1300G to 2000G. This is the standard value most ferrite based transformer cores. In this example, let’s settle at 1500G. So we have Bmax = 1500. Higher values of Bmax is not recommended as this may result in the transformer reaching saturation point. Conversely, lower values of Bmax may result in the core being underutilized.
- Ac = Effective Cross-Sectional Area in cm2. This information can be collected from the datasheets of the ferrite cores. You may also find Ac being presented as Ae. For the selected core number ETD39, the effective cross-sectional area furnished in the datasheet sheet is 125mm2. That is equal to 1.25cm2. Therefore we have, Ac = 1.25 for ETD39.
The above figures give us the values for all the parameters required for calcuating the primary turns of our SMPS inverter transformer. Therefore, substituting the respective values in the above formula, we get:
N(prim) = Vin(nom) x 108 / 4 x f x Bmax x AcN(prim) = 12 x 108 / 4 x 50000 x 1500 x 1.2 N(prim) = 3.2Since 3.2 is a fractional value and can be difficult to implement practically, we'll round it off to 3 turns. However, before finalizing this value, we have to investigate whether or not the value of Bmax is still compatible and within the acceptable range for this new rounded off value 3.
Because, decreasing the number of turns will cause a proportionate increase in the Bmax, therefore it becomes imperative to check if the increased Bmax is still within acceptable range for our 3 primary turns.
Counter checking Bmax by substituting the following existing values we get:
Vin(nom) = 12, f = 50000, Npri = 3, Ac = 1.25Bmax = Vin(nom) x 108 / 4 x f x N(prim) x Ac Bmax = 12 x 108 / 4 x 50000 x 3 x 1.25 Bmax = 1600As can be seen the new Bmax value for N(pri) = 3 turns looks fine and is well within the acceptable range. This also implies that, if anytime you feel like manipulating the number of N(prim) turns, you must make sure it complies with the corresponding new Bmax value.
Oppositely, it may be possible to first determine the Bmax for a desired number of primary turns and then adjust the number of turns to this value by suitably modifying the other variables in the formula.
Calculating the Secondary Turns
Now we know how to calculate the primary side of an ferrite SMPS inverter transformer, it's time to look into the other side, that is the secondary of the transformer.
Since the peak value has to be 310 V for the secondary, we would want the value to sustain for the entire battery voltage range starting from 13 V to 10.5 V.
No doubt we will have to employ a feedback system for maintaining a constant output voltage level, for countering low battery voltage or rising load current variations.
But for this there has to be some upper margin or headroom for facilitating this automatic control. A +20 V margin looks good enough, therefore we select the maximum output peak voltage as 310 + 20 = 330 V.
This also means that the transformer must be designed such that it can produce 310 V even at the lowest 10.5 battery voltage.
For feedback control we normally employ a self adjusting PWM circuit, which widens the pulse width during low battery or high load, and narrows it proportionately during no load or optimal battery conditions.
This means, at low battery conditions the PWM must auto adjust to maximum duty cycle, for maintaining the stipulated 310 V output. This maximum PWM can be assumed to be 98% of the total duty cycle.
The 2% gap is left for the dead time. Dead time is the zero voltage gap between each half cycle frequency, during which the MOSFETs or the specific power devices remain completely shut off.
This ensures guaranteed safety and prevents shoot through across the MOSFETs during the transition periods of the push pull cycles.
Hence, input supply will be minimum when the battery voltage reaches at its minimum level, that is when Vin = Vin(min) = 10.5 V. This will prompt the duty cycle to be at its maximum 98%.
The above data can be used for calculating the average voltage (DC RMS) required for the primary side of the transformer to generate 310 V at the secondary, when battery is at the minimum 10.5 V. For this we multiply 98% with 10.5, as shown below:
0.98 x 10.5 V = 10.29 V, this the voltage rating our transformer primary is supposed to have.
Now, we know the maximum secondary voltage which is 330 V, and we also know the primary voltage which is 10.29 V.
The turns ratio (n) can be calculated as:
n = Vs / VpSubstituting the given values:
n = 330 / 10.29 ≈ 32.1Since the turns ratio is equal to the voltage ratio, the number of turns on the secondary (Ns) and primary (Np) sides must maintain the same ratio.
This relationship is expressed as:
Ns / Np = nConsidering the primary side has 3 turns (Np = 3), we can solve for Ns:
Ns = n * NpSubstituting the values we get:
Ns = 32.1 * 3 = 96.3Therefore we get the number of secondary turns to be approximately 96.3.
The figure 96.3 is the number of secondary turns that we need for the proposed ferrite inverter transformer that we are designing. As stated earlier since fractional vales are difficult to implement practically, we round it off to 96 turns.
This concludes our calculations and I hope all the readers here must have realized how to simply calculate a ferrite transformer for a specific SMPS inverter circuit.
Calculating Auxiliary Winding
An auxiliary winding is a supplemental winding that a user may require for some external implementation.
Let's say, along with the 330 V at the secondary, you need another winding for getting 33 V for an LED lamp. We first calculate the secondary : auxiliary turn ratio with respect to the secondary winding 310 V rating. The formula is:
NA = Vsec / (Vaux + Vd) NA = secondary : auxiliary ratio, Vsec = Secondary regulated rectified voltage, Vaux = auxiliary voltage, Vd = Diode forward drop value for the rectifier diode. Since we need a high speed diode here we will use a schottky rectifier with a Vd = 0.5V
Solving it gives us:
NA = 310 / (33 + 0.5) = 9.25, let's round it off to 9.Now let's derive the number of turns required for the auxiliary winding, we get this by applying the formula:
Naux = Nsec / NA Where Naux = auxiliary turns, Nsec = secondary turns, NA = auxiliary ratio.
From our previous results we have Nsec = 96, and NA = 9, substituting these in the above formula we get:
Naux = 96 / 9 = 10.66, round it off gives us 11 turns. So for getting 33 V we will need 11 turns on the secondary side.
So in this way you can dimension an auxiliary winding as per your own preference.
Calculating the Wire Thickness
We can calculate the wire thickness by taking into account the current flowing through the primary and secondary windings.
The formula for current is:
Primary Current (Ip):
Ip = P / (Vp * η)Secondary Current (Is):
Is = P / (Vs * η)- Where:
- P = Output power of the SMPS (in watts)
- Vp = Primary voltage (in volts)
- Vs = Secondary voltage (in volts)
- η = Efficiency of the SMPS (typically around 0.8 to 0.9)
The current density (J) is the maximum current a wire can safely carry per unit cross-sectional area.
A typical value for SMPS applications is around 4-6 A/mm².
The cross-sectional area (A) of the wire is given by:
A = I / J- Where:
- I = Current (either Ip or Is)
- J = Current density (A/mm²)
The diameter of the wire can be calculated from the cross-sectional area by using the formula for the area of a circle:
A = (π * d²) / 4Rearranging for d:
d = √((4 * A) / π)- Where:
- d = Diameter of the wire (in mm)
- A = Cross-sectional area (in mm²)
For high-frequency SMPS designs, the RMS current and skin effect must be considered.
The skin depth (δ) informs us regarding how deeply current penetrates into the conductor and is given by:
δ = √(ρ / (π * f * μ))- Where:
- ρ = Resistivity of copper (typically 1.68 × 10-8 Ω·m)
- f = Operating frequency of the transformer (in Hz)
- μ = Permeability of copper (4π × 10-7 H/m)
For high-frequency designs it is recommended to use multiple thinner wires (litz wire) to minimize skin effect losses.
Now let us see how we can calculate the wire thickness for a 100 W SMPS transformer with the following parameters:
P = 100 W
Vp = 10.29 V
Vs = 330 V
η = 0.85
J = 5 A/mm²Primary Current:
Ip = P / (Vp * η)Ip = 100 / (10.29 * 0.85) ≈ 11.4 ACross-Sectional Area for Primary Wire:
Ap = Ip / JAp = 11.4 / 5 = 2.28 mm²Primary Wire Diameter:
dp = √((4 * Ap) / π)dp = √((4 * 2.28) / 3.1416) ≈ 1.7 mmSecondary Current:
Is = P / (Vs * η)Is = 100 / (330 * 0.85) ≈ 0.36 ACross-Sectional Area for Secondary Wire:
As = Is / JAs = 0.36 / 5 = 0.072 mm²Secondary Wire Diameter:
ds = √((4 * As) / π)ds = √((4 * 0.072) / 3.1416) ≈ 0.3 mmIf the operating frequency is high (e.g. 20 kHz or higher), consider using litz wire to reduce skin effect losses.
Make sure to use multiple strands of thinner wires with a combined cross-sectional area equal to the calculated area, and avoid using a single thick wire.
Wrapping up
In this post I have explained how to calculate and design ferrite core based inverter transformers, using the following steps:
- Calculate primary turns
- Calculate secondary turns
- Determine and Confirm Bmax
- Determine the maximum secondary voltage for PWM feedback control
- Find primary secondary turn ratio
- Calculate secondary number of turns
- Calculate auxiliary winding turns
Using the above mentioned formulas and calculations an interested user can easily design a customized ferrite core based inverter for SMPS application.
For questions and doubts please feel free to use the comment box below, I'll try to solve at an earliest
More Information can be found under this link:



pls sir I have issue in knowing how to use this ferite transformer for an inverter circuit . pls can you help clarify it, like knowing how to identify the primary, secondary and auxiliary in more ferite transformer thanks in advance
Sure Asikpo, you can try the following software tool to figure out the exact dimensions of the ferrite transformer:
https://www.homemade-circuits.com/smps-transformer-calculator-2/
hello dear, if I want to build 3kva SPWM Inverter, can I still use smps ferrite core transformer?
Hello Eromaka, you can use ferrite transformer for any inverter you wish to build…
halo pak, saya rencana ingin buat inverter mobil dc to dc 12 v to 42 v, berapa lilit kah untuk primer & skunder nya..? saya memakai ferit ukuran 5cm tebal 2mm. mohon jawabannya pak terimakasih
Hello Roni, you can take the help of this software for calculating all the parameters.
https://www.homemade-circuits.com/smps-transformer-calculator-2/
Hi
I want to know that whether the applied voltage to an smps is step down by the ferrite transformer or by the PWM IC. I it is done by IC but want to know the principle.
thanks
Silawar Khan
Hi, the ferrite transformer does the actual step-down of voltage but the PWM IC controls how much voltage and current the transformer gives to the output, and it does this by adjusting the duty cycle of the switching.
ok thanks.
Then it means duration of duty cycle is very very small of the complete cycle duration.
example is that , if applied voltage to ferrite transformer is 270 volt(DC) coming from capacitor and we have gain 12volt in output then duty cycle is 12/270*100=4.444% of the whole cycle.
Yes, that’s correct, the duty cycle will be proportional to the ratio of the output/input voltages.
https://www.homemade-circuits.com/smps-transformer-calculator-2/
Thanks for the lesson sir, always enjoy your lesson sir. But please sir, I don’t really understand some parts like how can I know the switching frequency the ferrite transformer can work with and I don’t really understand the wire size selection part sir. Please help me with that sir, because I’m working on one ferrite core transformer sir. Thanks sir.
You ae welcome Lukiz, I am glad you find my articles enjoyable and helpful.
The switching frequency will need to be selected by you, what suits best for your application. Higher frequency would mean smaller transformer and lower number of turns and vice vera.
For the wire size, you can take the help of the following post:
https://www.homemade-circuits.com/56492-2/
Ok thanks sir, but after the calculation base on your workings sir, 1.7mm wire gauge is bigger to use to wind even 3 turns for the ferrite core bobbin sir. Please help me with it sir.
Lukiz, you can use Litz type wire with many strands which are flexible and can be flattened and will fit inside the bobbin, or you may have to use a slightly bigger bobbin/core.
Thanks for always
Pls, I planned to make DC to DC 12v – 300v voltage voltage booster using push pull configuration.
So now, my push pull secondary side outputed voltage rating 900ACV, then I use UF5804 in form of bridge rectifier with additional 450v 47uf capacitor
But unfortunately my DC output is around 50DCV, which is very wrong
Pls help, am confused
Atiku, It seems your 900V AC reading is incorrect if the rectified DC is showing as 50V DC. Please recheck the AC voltage with a load connected.
If you are not getting 300V DC output, it means your winding calculations are not correct….
Please calculate them again, and check the response.
🤔🤔
I will try and check it😔
Sir, you’re so amazing
Your explanation is easy to understand, thanks a lot
Pls can I have your whatsapp contact, pls 🥺
Thank you so much Atiku, Glad you found my explanation helpful.
You can absolutely Feel free to discuss whatever circuit related issues you have on this comments platform, I will try to solve it for you as much as possible.
Pls I need a explanation on how to modify this Ac -DC 19v 3A adapter
To a 5.2v 50A
If you are looking for a switching regulator, then you can calculate the parameters as suggested in the following article:
https://www.homemade-circuits.com/calculating-inductor-value-in-smps/
This circuit you can use it at the output of your adaptor to get the 5.2V DC
50 amp is impossible from a 3A source…
Thanks I will go through it
Thank you Sir
sir this is incomplete information
please mantion transformer kw size wire size
or for 50khz frequency
500w tranformer core size
plz
Mahendra, I have updated the article with the required information…
shir hamko pcb banwana hai plese help 7607919707
Kanhaiya, sorry I do not manufacture PCB nowadays, you may have to find other online sources.