Notch Filter Calculator Tool

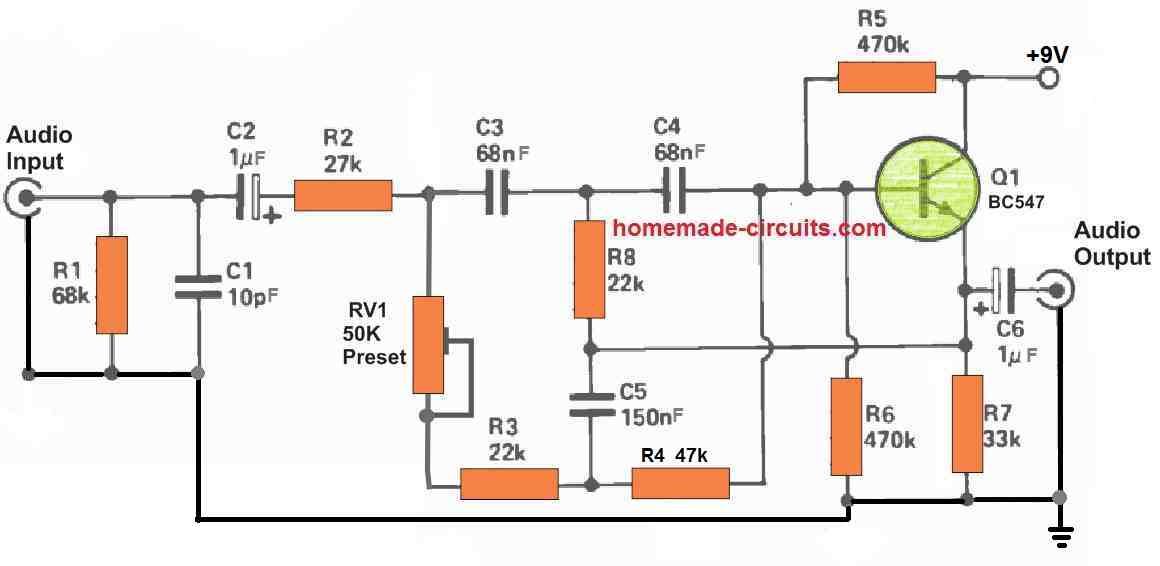
This small calculator is made for calculating notch filter frequency using the simple formula f = 1 / 2πR4C4 and as per the given circuit diagram below. We can also use the same calculator in reverse for finding R4 or C4 when the other two values are known to us.

We have three radio buttons so that we can select what we want to calculate... f, R4, or C4. When we select one of them, then code automatically hides and shows the proper input boxes according to that mode.

Then we have three main input areas:

1. R4 input area with its value box and unit dropdown (Ω, kΩ, MΩ).
2. C4 input area with its value box and unit dropdown (pF, nF, µF, etc).
3. Frequency input area with its value and unit (Hz, kHz, MHz).

When we select to calculate f, then it hides the frequency input, When we select to calculate R4 or C4, then it shows the frequency box and disables the one that we are going to calculate.

The Buttons Section

Then we see two buttons “Calculate” and “Reset”.
The Calculate button triggers the main math part inside the script.
The Reset button fills back default values for R4 = 10kΩ and C4 = 10nF and clears the result box.

1. When mode is f:
   Then we take R and C values, then multiply their unit multipliers and calculate frequency using f = 1 / (2 * π * R * C).
   Then it shows both numeric and formatted values on the screen.
2. When mode is r:
   Then we take f and C values and use the rearranged formula R = 1 / (2 * π * f * C).
   Then the result shows R4 in ohms and formatted value like kΩ or MΩ depending on result range.
3. When mode is c:
   Then we take f and R values and use the rearranged formula C = 1 / (2 * π * f * R).
   Then the result shows C4 in Farads with formatted readable format like µF or nF.

The code also checks for in-valid or missing values and displays an error message in red if any input is wrong or missing.

Practical Working Calculation

let us now take one clear manual example so that we can see how this notch filter calculator actually works using the formula f = 1 / (2πR4C4).

We will do the full step-by-step math manually just like the calculator would do it.

Example Situation

Let us say we have:
R4 = 10 kΩ
C4 = 10 nF

Now we want to find the notch (center) frequency f.

Step 1 – Convert All Values To Base Units

We must convert both R4 and C4 into ohms and farads first because the formula works only with SI base units.

So
R4 = 10 kΩ = 10 * 1000 = 10,000 Ω
C4 = 10 nF = 10 * 10⁻⁹ = 0.00000001 F

Step 2 – Apply The Formula

The main formula is:

f = 1 / (2 * π * R4 * C4)

Now let us substitute the values:

f = 1 / (2 * 3.1416 * 10000 * 0.00000001)

Step 3 – Do The Multiplications Step By Step

First, multiply R4 × C4:

10000 * 0.00000001 = 0.0001

Now multiply 2 * π * 0.0001:

2 * 3.1416 * 0.0001 = 0.00062832

Step 4 – Take The Reciprocal

Now divide 1 by 0.00062832:

1 / 0.00062832 ≈ 1592.5 Hz

Step 5 – Write The Final Answer

So for R4 = 10 kΩ and C4 = 10 nF,

f ≈ 1.59 kHz

That is the notch frequency.

Step 6 – Verify Reverse Calculation (Optional)

If we now want to find C4 from this frequency and resistance, we can reverse the formula:

C4 = 1 / (2π f R4)

Substitute f = 1592.5 Hz and R4 = 10,000 Ω

C4 = 1 / (2 * 3.1416 * 1592.5 * 10000)
C4 = 1 / 100,000,000 ≈ 1.0 × 10⁻⁸ F = 10 nF

So our math perfectly matches the forward calculation.

Step 7 – Summary Of Example

So in this example,
R4 = 10 kΩ
C4 = 10 nF
Then f = 1 / (2πR4C4) = 1592.5 Hz ≈ 1.6 kHz

That means the notch filter will have its center (cut) frequency at about 1.6 kHz.